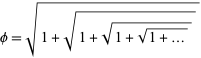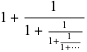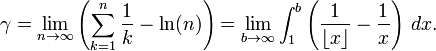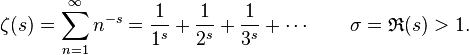|
|
|
MATHEMATICIANS (Also see
http://aleph0.clarku.edu/~djoyce/mathhist/chronology.html )
Pythagoras of Samos (c. 570-c. 495 BC):
(Greek)
He was an
Ionian
Greek
philosopher,
mathematician, and
founder of the religious movement called
Pythagoreanism. Most
of the information about Pythagoras was written down centuries after he
lived, so that very little reliable information is known about him.
Around 530 BC, he moved to
Croton, a
Greek colony in
southern Italy, and
there set up a religious sect. His followers pursued the religious rites and
practices developed by Pythagoras, and studied his philosophical theories.
The society took an active role in the politics of Croton, but this
eventually led to their downfall. The Pythagorean meeting-places were
burned, and Pythagoras was forced to flee the city. He is said to have ended
his days in
Metapontum. He is
often revered as a great
mathematician,
mystic and
scientist, and he is
best known for the
Pythagorean theorem
which bears his name.
Euclid of Alexandria (300 BC- ):
(Greek) He was often referred to as the
"Father of Geometry."
His "Elements" is one of the most influential works in mathematics,
serving as the main textbook for teaching mathematics, especially geometry,
from the time of its publication until the late 19th or early 20th century.
Euclid would
love the following web sites:
http://www.flixxy.com/missing-square-puzzle.htm#.UXvz1q7D8fc and
https://en.wikipedia.org/wiki/Missing_square_puzzle and
https://www.brainbashers.com/missinganswer.asp and
http://mathusiasts.wordpress.com/2011/04/16/missing-square-puzzle-solution/
but Fibonacci would have preferred
http://jaysdesktop.blogspot.com/2009/07/solution-to-missing-square-problem.html
Geometry
Are the eight balls
moving in a circle or a straight line?
http://showyou.com/v/y-pNe6fsaCVtI/crazy-circle-illusion?u=multimotion
Archimedes
of Syracuse (c.287-c.212 B.C): (from
Sicily) A mathematician and inventor. He determined the exact value of pi,
is also known for his strategic role in ancient war and the development of
military techniques.
"Give me a
place to stand and I will move the earth" was his boast when he
discovered the laws of levers and pulleys. His mechanical inventions
defeated the Roman fleet of Marcellus.
The word "eureka" comes from the story that when Archimedes figured out a
way to determine whether the king (Hiero II of Syracuse), a possible
relative, had been duped by measuring the buoyancy of the king's supposedly
solid gold crown in water, he became very excited and exclaimed the Greek
(Archimedes' native language) for "I have found it": Eureka.
Archimedes
requested that his tombstone be decorated with a sphere contained in
the smallest possible cylinder and inscribed with the ratio of the
cylinder's volume to that of the sphere. Archimedes considered the discovery
of this ratio the greatest of all his accomplishments.
Heron of Alexandria Not sure of when he
lived. Probably around 62 AD. Spent time in the Library of Alexandria.
Heron also proves his famous formula of the area, A, of a triangle knowing
the three sides is:
Heron's formula:
where
Given: the three sides
(s is called the
semiperimeter,
or half the triangle's perimeter) It has been suggested that
Archimedes knew the formula over two
centuries earlier. Other references:
www.math.umn.edu/~rejto/1151/1151_heron.pdf and mathworld.wolfram.com/HeronsFormula.html
Diophantus of Alexandria
(200 and 214 --
284 and 298): (Greek) Sometimes
called "the father of
algebra", was an
Alexandrian
Greek mathematician
and the author of a series of books called
Arithmetica.
These texts deal with solving
algebraic equations,
many of which are now lost. In studying Arithmetica.
Pierre de Fermat
concluded that a certain equation considered by Diophantus had no solutions,
and noted without elaboration that he had found "a truly marvelous proof of
this proposition," now referred to as
Fermat's Last Theorem.
This led to tremendous advances in
number theory, and
the study of
Diophantine equations
("Diophantine geometry") and of
Diophantine approximations
remain important areas of mathematical research. Diophantus was the first
Greek mathematician
who recognized fractions as numbers; thus he allowed
positive
rational numbers for
the coefficients and solutions. In modern use, Diophantine equations are
usually algebraic equations with
integer coefficients,
for which integer solutions are sought. Diophantus also made advances in
mathematical notation.
Leonardo Pisano Fibonacci (1170?-1250):
(Italian) Fibonacci is considered to be one of the most talented
mathematicians for the Middle Ages. Few people realize that it was Fibonacci
that gave us our decimal number system (Hindu-Arabic numbering system) which
replaced the Roman Numeral system. When he was studying mathematics, he used
the Hindu-Arabic (0-9) symbols instead of Roman symbols which didn't have
0's and lacked place value. In fact, when using the Roman Numeral system, an
abacus was usually required. There is no doubt that Fibonacci saw the
superiority of using Hindu-Arabic system over the Roman Numerals. He shows
how to use our current numbering system in his book Liber abaci. And
he gave us the Fibonacci Series. Fibonacci was known as Leonardo of
Pisa. He was born in Pisa, home of the famous leaning tower and his statue
is located there.
In his famous "Rabbit Problem" he produces the Fibonacci Series as the
answer: 1 1 2 3 5 8 13 21 34 55 etc., where each term is equal to the sum of
the two previous terms. The Fibonacci sequence obeys the recursion
relation F(n) = F(n-1) + F(n-2). The ratio of the current term to the
previous term approaches the golden ratio or (1 + sq rt of 5)/2, about
1.618... This ratio is called the "golden ratio". The German
Adolph Zeising claimed the front of the Parthenon is in proportion to the
golden ratio. There is no documentary evidence that Phidias, used the golden
ratio in any of his work related to the Parthenon. However around
1909, the American mathematician Mark Barr, named the golden ratio the Greek
letter "phi" for Phidias.. When phi is expressed as a continued
fraction it looks like this:
Continued fractions provide mathematicians with a way of rating how
irrational a number might be. Since the expression for phi contains only 1s,
it is the purest continued fraction that there is, and hence is
considered the most irrational number.
IRRATIONAL NUMBERS See
http://www.ams.org/samplings/feature-column/fcarc-irrational1
An irrational number by definition is one which cannot be written as
the ratio of whole numbers. So it would seem that all irrational numbers are
equally irrational. All pigs are equal, Orwell said, but some are
more equal than others. And in fact there is a precise sense in which
some irrational numbers are more irrational than others. This phenomenon has
had important consequences in the organization of the natural world. In
packing seeds around a core, many plants choose the strategy of placing each
one at the most irrational angle possible to the one directly below it.
The Pythagoreans did not believe in irrational numbers or
incommensurability. But in
we can look at a square with a and b equal to 1 and c = square root of 2.
One rectangle has a =1, c = 2, and b = square root of 3. Another
rectangle has a =1, b = 2, and c = square root of 5.
These irrational numbers are also found in other geometrical shapes.
The pentagram which contains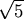 
. Sir Thomas Mallory in La Morte d'Arthur placed it on Sir
Gawain's shield. In Dan Brown'sThe Da Vinci Code, the dying curator
of the Louvre drew a pentagram in his own blood on his abdomen as a clue to
identify his murderer. The hexagram was also mentioned by Dan Brown in
the same novel. It contains √3,
which is the length of the shorter diagonal of a hexagram whose sides equal
1.
In studying "Sacred Geometry" (http://sacredgeometryinternational.com/the-meaning-of-sacred-geometry-part-3-the-womb-of-sacred-geometry#
)we see the Vessel of Fish. This diagram is usually shown as two identical
circles in which the right hand circle passes thru the center of the first
circle on the left. The square roots of 3 and 5 are included.
The many objects of Sacred Geometry may be achieved by means of the figure
known as the Vesica Piscis.
The most irrational number
The most irrational number turns out to be a number already well known in
geometry. It is the number
Phi =
= (
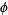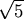+ 1)/2 = 1.618033...
which is the length of the diagonal in a regular pentagon of side length
1. This number, known as the "golden mean," has played a large role in
mathematical aesthetics. It is not clear whether its supreme irrationality
has anything to do with its artistic applications.
It is the only number that is 1 more than its reciprocal. x = 1/x
-1.
The golden mean satisfies the equation x2 - x - 1 = 0, so its
continued fraction expansion is the simplest of all:
A representation in terms of a
nested radical
is
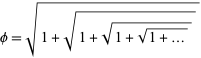
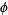is the "worst" real number for rational approximation because its continued
fraction is:
=
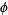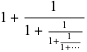
| The Fibonacci numbers are
0, 1, 1, 2, 3, 5, 8, 13, ...
(add
the last two to get the next)
The Golden Section numbers are
±0·61803 39887... and ±1·61803
39887...
Phi is the only number that is 1 less than
its reciprocal.
Phi -1 = 1/Phi
The Golden String is a fractal string of 0s and 1s that
grows in a Fibonacci-like way as follows:
1
10
101
10110
10110101
1011010110110
101101011011010110101 After the first
two lines, all the others are made from the two latest lines in a
similar way to each Fibonacci numbers being a sum of the two before
it. Each string (list of 0s and 1s) is a copy of the one above it
followed by the one above that. The resulting infinitely long string
is the Golden String or Fibonacci Word or Rabbit Sequence. It
is is closely related to the Fibonacci numbers and the golden
section. There is a relationship between fractals and the "golden
string". See
http://www.youtube.com/watch?v=ZDGGEQqSXew |
Leonardo Da Vinci
called the golden ratio the "divine proportion" and featured it in
many of his
paintings.
Nicolaus Copernicus (1473-1543):
(Prussia) He was a
Renaissance
astronomer and the
first person to formulate a comprehensive
heliocentric
cosmology, which
displaced the
Earth from the center
of the
universe.
Copernicus' epochal book,
De revolutionibus orbium coelestium
(On the Revolutions of the Celestial Spheres), published just before
his death in 1543, is often regarded as the starting point of modern
astronomy and the
defining
epiphany that began
the
scientific revolution.
His
heliocentric model,
with the Sun at the center of the universe, demonstrated that the observed
motions of celestial objects can be explained without putting Earth at rest
in the center of the universe. His work stimulated further scientific
investigations, becoming a
landmark in the
history of science
that is often referred to as the
Copernican Revolution.
Niccolò Fontana "Tartaglia" (1499/1500-1557):
(Italian) He published many books, including the first Italian
translations of
Archimedes and
Euclid, and an acclaimed compilation of
mathematics. Tartaglia was the first to
apply mathematics to the investigation of the paths of cannonballs, known as
ballistics, in his
Nova Scientia, “A New Science;” his work
was later validated by
Galileo's studies on falling bodies. He
also published a treatise on retrieving sunken ships.
When the French invaded Brescia, a French soldier sliced Niccolò's jaw
and palate with a saber. This made it impossible for Niccolò to speak
normally, prompting the nickname "Tartaglia" ("stammerer"), which he
adopted.
His best known work is his treatise General Trattato di numeri, et
misure published in Venice 1556–1560. This has been called the best
treatise on
arithmetic that appeared in the sixteenth century.
Not only does Tartaglia have complete discussions of numerical
operations and the commercial rules used by Italian arithmeticians in this
work, but he also discusses the life of the people, the customs of merchants
and the efforts made to improve arithmetic in the 16th century.
Tartaglia is known for his conflicts with
Gerolamo Cardano. Cardano cajoled Tartaglia into revealing the solution
to the
cubic equations, by promising not to publish them. Tartaglia divulged
the secrets of the solutions of three different forms of the cubic equation
in verse. Even though Cardano credited his discovery, Tartaglia was
extremely upset. He responded by publicly insulting Cardano.
Mathematical historians now credit both with the paternity of the formula to
solve cubic equations, referring to it as the "Cardano-Tartaglia Formula".
Gerolamo
Cardano (1501-1576): (French) He
was an
Italian
Renaissance
mathematician,
physician,
astrologer and
gambler. Today, he is
best known for his achievements in
algebra. He published
the solutions to the
cubic and
quartic equations in
his 1545 book
Ars Magna. The
solution to one particular case of the cubic, x3 + ax =
b (in modern notation), was communicated to him by
Niccolo Fontana Tartaglia
(who later claimed that Cardano had sworn not to reveal it, and engaged
Cardano in a decade-long fight), The quartic was solved by Cardano's student
Lodovico Ferrari.
Both were acknowledged in the foreword of the book, as well as in several
places within its body. In his exposition, he acknowledged the existence of
what are now called
imaginary numbers,
although he did not understand their properties (Mathematical field theory
was developed centuries later). In Opus novum de proportionibus he
introduced the
binomial coefficients
and the
binomial theorem.
Cardano was notoriously short of money and kept
himself solvent by being an accomplished gambler and
chess player. His
book about games of chance, Liber de ludo aleae ("Book on Games of
Chance") , written in 1526, but not published until 1663, contains the first
systematic treatment of
probability, as well
as a section on effective cheating methods. Cardano invented several
mechanical devices including the
combination lock, the
gimbal consisting of
three concentric rings allowing a supported
compass or
gyroscope to rotate
freely, and the
Cardan shaft with
universal joints,
which allows the transmission of rotary motion at various angles and is used
in vehicles to this day. He studied
hypocycloids,
published in de proportionibus 1570. The generating circles of these
hypocycloids were later named Cardano circles or cardanic circles and were
used for the construction of the first high-speed
printing presses.
Franciscus
Vieta (1540-1603):
(French)
His work on
new algebra was an
important step towards modern algebra, due to its innovative use of letters
as parameters in equations. He was a lawyer by trade, and served as a
privy councillor to
both
Henry III and
Henry IV.
Galileo
Galilei(1564-1642):
(Italian) A
physicist,
mathematician,
astronomer and
philosopher who
played a major role in the
Scientific Revolution.
His achievements include improvements to the
telescope and
consequent astronomical observations, and support for
Copernicanism.
Galileo has been called the "father of modern observational
astronomy", the
"father of modern
physics", the "father
of
science", and "the
Father of Modern Science".
Stephen Hawking says,
"Galileo, perhaps more than any other single person, was responsible for the
birth of modern science." Read about his "square cube" law:
http://dinosaurtheory.com/scaling.html
Johannes Kepler (1571-1630):
(German)
A
mathematician,
astronomer and
astrologer, and key
figure in the 17th century
scientific revolution.
He is best known for his
eponymous
laws of planetary motion,
codified by later astronomers, based on his works
Astronomia nova,
Harmonices Mundi,
and
Epitome of Copernican Astronomy.
These works also provided one of the foundations for
Isaac Newton's theory
of
universal gravitation.
Rene Descartes
(1596-1650): (French) The inventor of Analytical Geometry.
He was a philosopher, mathematician, physicist and writer. He has been
dubbed the "Father of Modern Philosophy". If
you want interesting info on conic sections, see
https://mysite.du.edu/~jcalvert/ (James B Calvert is a retired
professor of Engineering at the University of Denver and has an excellent
web site).
Pierre de Fermat (1601-1665):
(French) A lawyer and amateur mathematician who contributed to Number
Theory and known for "Fermat's Last Theorem". Fermat was the
first person known to have evaluated the integral of general power
functions. Using an ingenious trick, he was able to reduce this evaluation
to the sum of geometric series. The resulting formula was helpful to both
Newton and Leibnitz in developing calculus.
John Wallis (1616-1703): (English)
A mathematician
who is given partial credit for the development of
infinitesimal calculus.
Between 1643 and 1689 he served as chief
cryptographer for
Parliament and,
later, the royal court. He is also credited with introducing the
symbol ∞ for
infinity.
Wallis made significant contributions to
trigonometry,
calculus,
geometry, and the
analysis of
infinite series. In
his Opera Mathematica I (1695) Wallis introduced the term "continued
fraction". He is generally credited
as the originator of the idea of the
number line where
numbers are represented geometrically in a line with the positive numbers
increasing to the right and negative numbers to the left. In 1655,
Wallis published a treatise on
conic sections in
which they were defined analytically. This was the earliest book in which
these curves are considered and defined as curves of the second degree. It
helped to remove some of the perceived difficulty and obscurity of
Rene Descartes' work
on
analytic geometry.
Arithmetica Infinitorum, the most important of Wallis's works, was
published in 1656. In this treatise the methods of analysis of Descartes and
Cavalieri were
systematised and extended. in 1659, Wallis published a tract
containing the solution of the problems on the
cycloid which had
been proposed by
Blaise Pascal. In
this he incidentally explained how the principles laid down in his
Arithmetica Infinitorum could be used for the rectification of algebraic
curves; and gave a solution of the problem to rectify (i.e. find the length
of) the semi-cubical parabola x3 = ay2,
which had been discovered in 1657 by his pupil
William Neile. Since
all attempts to rectify the ellipse and hyperbola had been (necessarily)
ineffectual, it had been supposed that no curves could be rectified, as
indeed Descartes had definitely asserted to be the case. The
logarithmic spiral
had been rectified by
Evangelista Torricelli,
and was the first curved line (other than the circle) whose length was
determined, but the extension by Neil and Wallis to an algebraic curve was
novel. The cycloid was the next curve rectified; this was done by
Wren in 1658.
Blaise Pascal (1623-1662): (French) He
helped create two major new areas. He wrote a significant treatise on
projective geometry at the age of sixteen. Pascal's
development of probability theory was his most influential contribution to
mathematics, a subject on which he corresponded with Fermat. Pascal
continued to influence mathematics throughout his life. In 1653 he described
a convenient tabular presentation for binomial coefficients, now called
Pascal's triangle.
Sir Isaac Newton (1643-1727):
(British) His theory of gravity unified the force that keeps our feet
on the ground, with the force that holds planets in their orbits. His 1687
publication of the
Philosophiae Naturalis Principia Mathematica is considered to be
among the most influential books in the history of science. In this
work, Newton described universal gravitation and the three laws of
motion. Newton shares the credit with Leibnitz for the development of
differential and integral calculus. He also demonstrated the generalized
binomial theorem and contributed to the study of power series.
Gottfried Wilhelm Leibnitz (1646-1716):
(German) He invented infinitesimal calculus independently of Newton,
and his notation has been in general use since then. He also invented the
binary system, the foundation of virtually all modern computer
architectures.
Bernoulli Family of Swiss Mathematicians: Three
were : Jacob Bernoulli (1654-1705),
his brother
Johann Bernoulli (1667-1748) and Johann's son
Daniel Bernoulli (1700-1787).
Jacob wrote the Art of Conjecture.
In this work, he described the known results in probability theory and in
enumeration, often providing alternative proofs of known results. This work
also includes the application of probability theory to games of chance and
his introduction of the theorem known as the law of large numbers. The terms
Bernoulli trial and
Bernoulli numbers result from this work. He.chose a figure of a
logarithmic spiral and the motto Eadem mutata resurgo ("Changed and
yet the same, I rise again") for his gravestone. He called it the
spiral mirabilis, the wonderful spiral. The spiral executed by the
stonemasons was, however, an Archimedean spiral. Just
like a fractal, a logarithmic spiral is self similar: That is, any
smaller piece of a larger spiral is identical in shape to the larger piece.
Johann studied the function y = xx
and he also investigated series using the method of integration by parts.
Integration to Bernoulli was simply viewed as the inverse operation to
differentiation and with this approach he had great success in integrating
differential equations. He summed series, and discovered addition theorems
for trigonometric and hyperbolic functions using the differential equations
they satisfy. Johann was known as the "Archimedes of his age" and this is
indeed inscribed on his tombstone.
Daniel was a Dutch Swiss
mathematician. He is particularly remembered for his applications of
mathematics to mechanics, especially fluid mechanics and for his pioneering
work in probability and statistics. Bernoulli's work is still studied at
length by many schools of science throughout the world. The Bernoulli
Principle that was used to explain lift applicable to airplane wings was
developed by Daniel Bernoulli.
Thomas Bayes (1702-1761):
An
English
mathematician,
statistician and
Presbyterian
minister, known for having formulated a specific case of the theorem that
bears his name. Bayes never published what would become his most
famous accomplishment. His notes were edited and published after his
death by
Richard Price.
Bayes Theorem deals with "conditional probabilities".
http://plato.stanford.edu/entries/bayes-theorem/
There were prominent mathematicians that did not embrace the logic of Bayes
Theorem .
ead Sharon Birtsch McGraynes book on "The Theory That Would Not Die" and see
her on
http://www.youtube.com/watch?v=8oD6eBkjF9o
Also her book is summarized on
http://www.nytimes.com/2011/08/07/books/review/the-theory-that-would-not-die-by-sharon-bertsch-mcgrayne-book-review.html?pagewanted=all&_r=0
Also read History:
http://lesswrong.com/lw/774/a_history_of_bayes_theorem/
Leonhard Euler
(1707-1783): One of his many contributions was called
"Euler's Formula". The formula states that, for any real
number x,
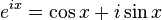where e is the base of the natural logarithm, i is the
imaginary unit, and cos and sin are the trigonometric functions, with the
argument x given in radians. The formula is still valid if x
is a complex number. Richard Feynman called Euler's formula "our
jewel" and "one of the most remarkable, almost astounding, formulas in all
of mathematics".
Euler Line
In the 18th century, the Swiss mathematician Leonhard Euler noticed that
three of the
centers of a triangle are always
collinear (they always lie on a straight line). The three centers that
have this surprising property are the triangle's
centroid (where the three
medians of the triangle's sides meet),
circumcenter (where the
perpendicular bisectors of the triangle's sides meet) and the
orthocenter (where the three
altitudes to the vertices of the triangle meet). The distance
from the orthocenter to the centroid is two times the distance from the
centroid to the circumcenter. (Another center, the
incenter, where the bisectors of the three angles meet, is not on
this line.)
 |
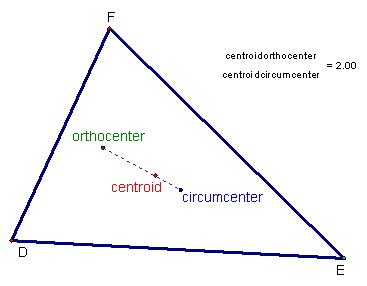| Acute Triangle |
 |
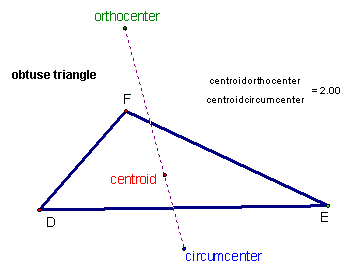| Obtuse Triangle |
 |
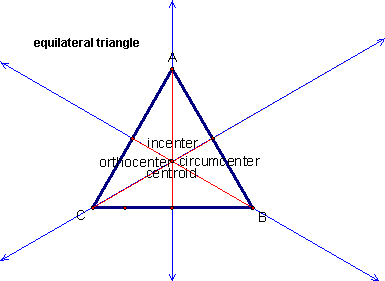| Equilateral Triangle |
Euler and the Nine Point Circle
The nine-point circle is a circle that can be constructed for any
given triangle. It is so named because it passes through nine significant
concyclic points defined from the triangle. These nine points are:
The nine-point circle is also known as Feuerbach's circle,
Euler's circle, and Terquem's circle.
To construct the nine point circle of a triangle, see
http://jwilson.coe.uga.edu/EMT668/EMT668.Folders.F97/Anderson/geometry/geometry1project/construction/construction.html
.1. Draw a triangle ABC and construct the midpoints of the three sides.
Label them as L, M, N.
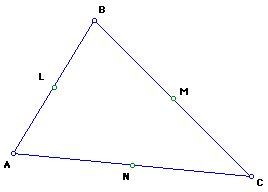
2. Construct the feet of the altitudes of the triangle ABC.
Label them as D, E, F. Label the point of intersection of the three
altitudes as H. This is also called the orthocenter.
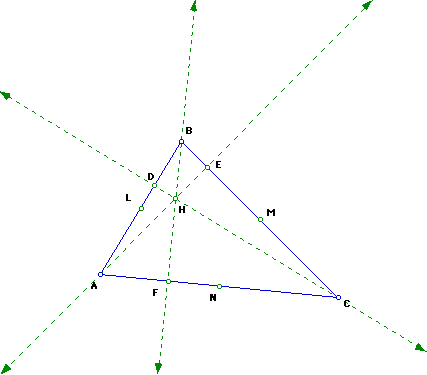
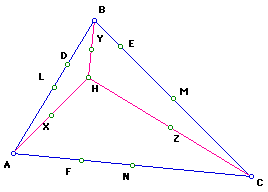
3. Construct the midpoints of the segments AH, BH, CH. Label
them as X, Y, Z.
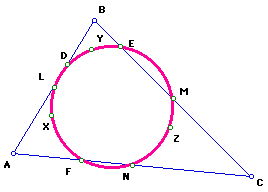
4. Notice the nine points, L,M,N,D,E,F,X,Y, Z, lie in a circle called the
Nine-Point Circle..
5. Construct the circumscribed circle for triangle
LMN. Label the center of that circle U.
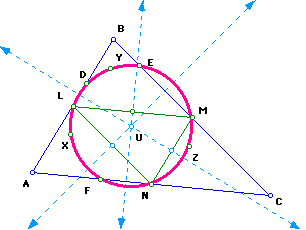
The center U of the circumscribed circle for triangle LMN will also be
the center of the Nine-Point Circle.
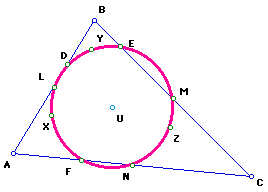
More on Nine-Point Circle at
http://en.wikipedia.org/wiki/Triangle_center where we learn
the following:
Let A, B, C denote
the vertex angles of the reference triangle, and let x : y : z be
a variable point in trilinear
coordinates;
then an equation for the Euler line is
-
| Center |
Trilinear Coordiates |
On Euler Line? |
| Orttocenter |
Secant A: Secant B : Secant C |
Yes |
| Centroid |
Cosecant A: Cosecant B: Cosecant C |
Yes |
| Circumcenter |
Cosine A: Cosine B: Cosine C |
Yes |
| Nine Point Circle |
Cosine (B - C): Cosine (C - A): Cosine (A
- B) |
Yes |
| In Center |
1:1:1 |
Only if Isosceles |
Euler and polyhedrons
A platonic solid is a
regular,
convex
polyhedron with
congruent
faces of
regular
polygons and the same number of faces
meeting at each
vertex. There are five regular
polyhedrons that meet those criteria, and each is named after its
number of faces.:
Euler's formula for polyhedrons is: V - E + F = 2 That
is the number of vertices, minus the number of edges, plus the number of
faces, is equal to two.
More on Euler
In
analytical mathematics,
Euler's identity (also known as Euler's equation) is the
equality:
Euler's number
e
is an important
mathematical constant,
approximately equal to 2.71828, that is the base of the
natural logarithm.
It is the
limit of
(1 + 1/n)n as
n becomes large, an expression that
arises in the study of
compound interest,
and can also be calculated as the sum of the infinite
series:
e
is the unique
real number such that
the value of the
derivative (slope of
the
tangent line) of the
function f(x) = ex
at the point x = 0 is equal to 1. The
function ex so defined
is called the
exponential function,
and its
inverse is the
natural logarithm, or
logarithm to
base
e.
The number
e is of eminent importance in mathematics, alongside
0,
1,
π
and
i.
All five of these numbers play important and recurring roles across
mathematics, and are the five constants appearing in one formulation of
Euler's identity.
Like the constant π, e
is
irrational: it is not
a ratio of
integers; and it is
transcendental: it is
not a root of any non-zero
polynomial with
rational coefficients. The numerical value of e
truncated to 50
decimal places is
2.71828182845904523536028747135266249775724709369995...
The Euler–Mascheroni constant (also called Euler's constant)
is a
mathematical constant
recurring in
analysis and
number theory,
usually denoted by the lowercase Greek letter
 (Gamma).
It is defined as the
limiting difference
between the
harmonic series and
the
natural logarithm:
-
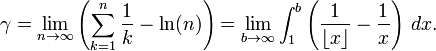
Here,
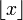represents the
floor function. The
numerical value of this constant, to 50 decimal places, is 0.57721566490153286060651209008240243104215933593992
... Euler established this formula in 1734. It is outrageous that we
cannot decide if
is a rational number or not. Even though over 1,000,000 digits
of this number have been calculated, it is not yet known if it is a
rational number (the ratio of two integers a/b). But if it
is rational, the denominator (b) must have more than 244,663 digits!
The sum of the reciprocals of all integers: 1/1 +1/2 +
1/3+ 1/4 + 1/5 + 1/6+ 1/7 etc equals Ln(N) + Gamma
The sum of the reciprocals of the odd integers: 1 + 1/3 + 1/5 + 1/7
etc equals {Ln(N) + Ln(2) + Gamma}/2
The sum of the reciprocals of the even integers: 1/2
+1/4+1/6+1/8 etc equals {Ln(N) -Ln(2) - Gamma}/2
The Basel problem is a famous problem in
mathematical analysis with relevance to
number theory, first posed by
Pietro Mengoli in 1644 and solved by
Leonhard Euler in 1735. Since the problem
had withstood the attacks of the leading
mathematicians of the day, Euler's solution
brought him immediate fame when he was twenty-eight. Euler generalised the
problem considerably, and his ideas were taken up years later by
Bernhard Riemann in his seminal 1859 paper
On the Number of Primes Less Than a Given Magnitude,
in which he defined his
zeta function and proved its basic
properties. The problem is named after
Basel, hometown of Euler as well as of the
Bernoulli family who unsuccessfully
attacked the problem.
The Basel problem asks for the precise
summation of the
reciprocals of the
squares of the
natural numbers, i.e. the precise sum of
the
infinite series:
-
The series is approximately equal to 1.644934. The Basel problem
asks for the exact sum of this series (in
closed form), as well as a
proof that this sum is correct. Euler found
the exact sum to be π2/6 and announced this discovery in
1735. His arguments were based on manipulations that were not justified at
the time, and it was not until 1741 that he was able to produce a truly
rigorous proof.
Read: "All about e" at
http://www.maa.org/sites/default/files/pdf/upload_library/22/Chauvenet/mccartin.pdf
Joseph-Louis Lagrange (1736-1813): (Italian)
Lagrange was one of the creators of the
calculus of variations,
deriving the
Euler Lagrange equations.
Lagrange invented the method of solving
differential equations
known as
variation of parameters,
applied
differential calculus
to the
theory of probabilities
and attained notable work on the solution of
equations. He proved
that
every natural number is a sum of four squares.
His treatise Theorie des fonctions analytiques laid some of the
foundations of
group theory,
anticipating
Galois. In
calculus, Lagrange
developed a novel approach to
interpolation and
Taylor series. He
studied the
three-body problem
for the Earth, Sun, and Moon and the movement of Jupiter's
satellites. In 1772 found the special-case solutions to this problem that
are now known as
Lagrangian points. He
transformed
Newtonian mechanics
into a branch of analysis,
Lagrangian mechanics
as it is now called. One of Lagrange's more famous books is the
Analytical Mechanics, which, he boasted proudly, contains no pictures.
Caspar Wessel (1745-1818):
(Danish-Norwegian) Wessel was a mathematician who was born in Norway.
In 1763, having completed secondary school, he went to Denmark for further
studies (Norway having no university at the time). In 1778 he acquired
the degree of
candidatus juris.
From 1794, however, he was employed as at
ttp://www.maa.org/sites/default/files/pdf/upload_library/22/Chauvenet/mccartin.pdf
surveyor (from 1798 as Royal inspector of
Surveying).
It was the mathematical aspect of surveying that
led him to exploring the geometrical significance of
complex numbers. His
fundamental paper, Om directionens analytiske betegning, was
published in 1799 by the
Royal Danish Academy of Sciences and Letters.
Since it was in Danish, it passed almost unnoticed, and the same results
were later independently found by
Argand and
Gauss.
One of the more prominent ideas presented in "On
the Analytical Representation of Direction"
was that of
vectors. Even though
this wasn't Wessel's main intention with the publication, he felt that a
geometrical concept of numbers, with length and direction, was needed.
Wessel's approach on addition was: "Two straight lines are added if we unite
them in such a way that the second line begins where the first one ends and
then pass a straight line from the first to the last point of the united
lines. This line is the sum of the united lines". This is the same idea as
used today when summing vectors.
Wessel's priority to the idea of a complex number
as a point in the
complex plane is
today universally recognized. His paper was re-issued in French translation
in 1899, and in English in 1999 as "On the analytic representation of
direction".
Pierre-Simon, marquis de Laplace (1749-1827):
(French) He is remembered as one of the greatest
scientists of all time, sometimes referred to as a
French
Newton or
Newton of France, with a phenomenal natural mathematical faculty
superior to any of his contemporaries. Laplace's writing of
Celestial Mechanics, an enormous, five volume tome of celestial
mechanics, established him as the Prince of Celestial Mechanicians. When
presented with a copy of some of the initial volumes, Napoleon is said to
have remarked, "I see no mention of God in this work". Laplace is said to
have replied, "Sir, I have no need of that hypothesis." (In an addition to
the story, the tale was related to Lagrange, who added "Ah, but it is such a
beautiful hypothesis; it explains a great many things!"
Jean Baptiste Joseph Fourier (1768-1830):
(French) A mathematician and physicist best known for initiating
the investigation of
Fourier series and their applications to
problems of
heat transfer and
vibrations. The
Fourier transform and
Fourier's Law are
also named in his honour. Fourier is also generally credited with the
discovery of the
greenhouse effect.
Carl Friedrich Gauss (1777-1855): (German)
Called the Prince of Mathematicians and the greatest mathematician
since antiquity. He is ranked as one of history's most influential
mathematicians. He referred to mathematics as the Queen of Sciences.
Gauss proved the Fundamental Theorem of Algebra. Gauss claimed
to have discovered the possibility of non Euclidean Geometries but never
published it.
Simeon Denis
Poisson
(1781-1840): (French) A
mathematician,
geometer, and
physicist. In
probability theory
and
statistics, the
Poisson distribution (or Poisson law of small numbers) is a
discrete probability distribution
that expresses the probability of a number of events occurring in a fixed
period of time if these events occur with a known average rate and
independently of the
time since the last event. (The Poisson distribution can also be used for
the number of events in other specified intervals such as distance, area or
volume.)
Baron
Augustin-Louis Cauchy (1789-1857):
(
French) He was an
early pioneer of
analysis. He started
the project of formulating and proving the theorems of
infinitesimal calculus
in a rigorous manner. He also gave several important theorems in
complex analysis and
initiated the study of
permutation groups in
abstract algebra. A
profound mathematician, Cauchy exercised a great influence over his
contemporaries and successors. His writings cover the entire range of
mathematics and
mathematical physics.
Michael Faraday (1791-1867) and James Clerk Maxwell (1831-1879):
They proved that electric and magnetic forces are the same force in
different guises.
Nikolai Ivanovich Lobachevsky (Никола́й
Ива́нович Лобаче́вский) (1792-1856):
(Russian)
A
mathematician and
geometer, renowned
primarily for his pioneering works on
hyperbolic geometry.
Niels Henrik Abel (1802-1829):
(Norwegian) At the age of 16, Abel gave a proof of
the
binomial theorem
valid for all numbers, extending Euler's result which had only held for
rational numbers. At age 19, he showed there is no general algebraic
solution for the roots of a quintic equation, or any general polynomial
equation of degree greater than four, in terms of explicit algebraic
operations. To do this, he invented (independently of Galois) an extremely
important branch of mathematics known as
group theory, which
is invaluable not only in many areas of mathematics, but for much of physics
as well. Among his other accomplishments, Abel wrote a monumental work on
elliptic functions which, however, was not discovered until after his death.
When asked how he developed his mathematical abilities so rapidly, he
replied "by studying the masters, not their pupils."
Janos Bolyai (1802-1860):
(Hungarian)
He was known for his work in
non-Euclidean geometry.
Between 1820 and 1823 he prepared a treatise on a complete system
of
non-Euclidean geometry.
Bolyai's work was published in 1832 as an appendix to a mathematics
textbook by his father.
Gauss, on reading the Appendix, wrote to a friend saying "I regard this
young
geometer Bolyai as a genius of the first order". In 1848 Bolyai
discovered not only that
Lobachevsky had published a similar piece of work in 1829, but also a
generalization of this theory. As far as is known, Lobachevsky published
his work a few years earlier than Bolyai, but it contained only hyperbolic
geometry. Bolyai and Lobachevsky did not know each other or each other's
works. In addition to his work in the geometry, Bolyai developed a rigorous
geometric concept of
complex numbers as
ordered pairs of
real numbers.
Although he never published more than the 24 pages of the Appendix,
he left more than 20,000 pages of mathematical manuscripts when he died.
Carl Gustav Jacob Jacobi (1804-1851)
(German) A
mathematician, widely considered to be the
most inspiring teacher of his time and one of the greatest mathematicians of
all time. One of Jacobi's greatest accomplishments was his theory of
elliptic functions.
He also made fundamental contributions in the study of differential
equations. It was in algebraic development that Jacobi's peculiar
power mainly lay, and he made important contributions of this kind to many
areas of mathematics, as shown by his long list of papers in Crelle's
Journal and elsewhere from 1826 onwards. One of his maxims was: 'Invert,
always invert' ('man muss immer umkehren'), expressing his belief that the
solution of many hard problems can be clarified by re-expressing them in
inverse form. He was also one of the early founders of the theory of
determinants.
Johann Peter Gustav Lejeune Dirichlet
(1805-1859): (German) He was credited with the modern formal
definition of a
function.
Dirichlet's brain is preserved in the anatomical collection of the
University of Gottingen, along with the brain of Gauss.
Sir William Rowan Hamilton
(1805-1865): (Irish)
A
physicist,
astronomer, and
mathematician, who
made important contributions to
classical mechanics,
optics, and
algebra. His studies
of mechanical and optical systems led him to discover new mathematical
concepts and techniques. His greatest contribution is perhaps the
reformulation of
Newtonian mechanics,
now called
Hamiltonian mechanics.
This work has proven central to the modern study of classical field theories
such as
electromagnetism, and
to the development of
quantum mechanics. In
mathematics, he is perhaps best known as the inventor of
quaternions. A
striking feature of quaternions is that the product of two
quaternions is
noncommutative,
meaning that the product of two quaternions depends on which factor is to
the left of the multiplication sign and which factor is to the right.
Hamilton defined a quaternion as the
quotient of two
directed lines in a three-dimensional space or equivalently as the quotient
of two
vectors. It can also
be represented as the sum of a scalar and a vector.
http://en.wikipedia.org/wiki/Quaternion
In four-dimensioal space the tesseract, or
hype, is the
four-dimensional
analog of the
cube. The tesseract
is to the cube as the cube is to the
square. Just as the
surface of the cube consists of 6 square
faces, the
hypersurface of the tesseract consists of 8 cubical
cells. The tesseract
is one of the six
convex regular 4-polytopes.
A generalization of the cube to dimensions greater than three is called a
"hypercube",
"n-cube" or "measure
polytope". The
tesseract is the four-dimensional hypercube' See
http://en.wikipedia.org/wiki/Fourth_dimension
Joseph Liouville (1809-1882):
(French) Liouville worked in a number of different
fields in mathematics, including
number theory,
complex analysis,
differential geometry and topology,
but also
mathematical physics
and even
astronomy. He is
remembered particularly for
Liouville's theorem,
a nowadays rather basic result in complex analysis. In number theory,
he was the first to prove the existence of
transcendental numbers
in 1844
by a construction using
continued fractions (Liouville
numbers). In mathematical physics,
Liouville made two fundamental contributions: the
Sturm Liouville theory,
which was joint work with
Charles Francois Sturm,
and is now a standard procedure to solve certain types of
integral equations by
developing into eigenfunctions, and the fact (also known as
Liouville's theorem)
that time evolution is measure preserving for a
Hamiltonian system.
In Hamiltonian dynamics, Liouville also introduced the notion of
action-angle variables
as a description of completely
integrable systems.
The modern formulation of this is sometimes called the Liouville-Arnold
theorem, and the underlying concept of integrability is referred to as
Liouville integrability.
The
following number
is
known as Liouville's constant.
(The exponent is negative j factorial.)
Liouville's constant is a decimal fraction with
1"s and 0"s in each decimal place. In1844 he constructed an infinite class
of
transcendental numbers
using
continued fractions,
but the above number was the first decimal constant
to be proven by Liouville in 1850 to be
transcendental.
Cantor subsequently proved that "almost all" real numbers are in fact
transcendental.
The crater
Liouville on the
Moon is named after him. So is the
Liouville function, an important function
in number theory. See
http://mathworld.wolfram.com/LiouvilleFunction.html
Ernst Eduard Kummer (1810 – 1893):
(German)
Skilled in applied
mathematics,
Kummer trained German army officers in
ballistics;
afterwards, he taught for 10 years in a gymnasium,
the German equivalent of high school, where he inspired the mathematical
career of Leopold
Kronecker.
Kummer made several contributions to mathematics in different areas; he
codified some of the relations between different hypergeometric
series,
known as contiguity relations. The Kummer
surface results
from taking the quotient of a two-dimensional abelian
variety by
the cyclic group {1, −1} (an early orbifold:
it has 16 singular points, and its geometry was intensively studied in the
nineteenth century). Kummer also proved Fermat's
last theorem for
a considerable class of prime exponents (see regular
prime, ideal
class group).
His methods were closer, perhaps, to p-adic ones
than to ideal
theory as
understood later, though the term 'ideal' arose here. He studied what were
later called Kummer
extensions of fields:
that is, extensions generated by adjoining an nth root to a field
already containing a primitive nth root
of unity.
This is a significant extension of the theory of quadratic extensions, and
the genus theory of quadratic
forms (linked
to the 2-torsion of the class group). As such, it is still foundational for class
field theory. Evariste Galois (1811-1832):
A symmetry of an object is what you can do to an object to leave it
essentially looking like it did before you touched it. Galois was
interested in the collection of all symmetries and seeing what happens if
you do one symmetry after another. He discovered that it is the
interactions between the symmetries in a group that encapsulate the
essential qualities of the symmetry of an object. Mathematicians
struggled for centuries to find formulas for the solutions of equations of
higher degree, but despite the efforts of
Euler, Bezout, Malfatti,
Lagrange, and others, no general solutions
were found. Finally,
Ruffini (1799)
and
Abel (1826) showed that the solution of the
general quintic cannot be written as a finite formula involving only the
four arithmetic operations and the extraction of roots. Galois developed the
theory of Galois groups and described exactly when a polynomial equation is
solvable.
Pierre Wantzel (1814 - 1848): (French)
He proved several ancient
geometric problems were
impossible to solve using only
compass and straightedge.
In a paper from 1837,
Wantzel proved that the problems
of
doubling the cube, and
trisecting the angle
are impossible to solve if one uses only
compass and straightedge.
In the same paper he also solved the problem of determining which
regular polygons are constructible:
a regular polygon is constructible
if and only if the number
of its sides is the product of a
power of two and any number
of distinct
Fermat primes (i.e. that
the sufficient conditions given by
Carl Friedrich Gauss are
also necessary).
Karl Theodor Wilhelm Weierstrass
(1815-1897): (German) He is often cited as the "father of modern
analysis".
George Boole
(1815-1864): (English) A
mathematician and
philosopher. As the
inventor of
Boolean logic, the
basis of modern digital
computer logic, Boole
is regarded in hindsight as a founder of the field of
computer science.
Boole said: " ... no general method for the solution of questions in
the theory of probabilities can be established which does not explicitly
recognise ... those universal laws of thought which are the basis of all
reasoning".
Arthur Cayley (1821-1895):
(British) He helped found the modern British school of
pure mathematics. He
proved the
Cayley-Hamilton theorem:
that every square
matrix is a root of
its own
characteristic polynomial.
He was the first to define the concept of a
group in the modern
way: as a set with a
binary operation
satisfying certain laws. Formerly, when mathematicians spoke of "groups",
they had meant
permutation groups.
Charles Hermite
(1822-1901):
(French)
He did research on
number theory,
quadratic forms,
invariant theory,
orthogonal polynomials,
elliptic functions,
and
algebra.
Hermite polynomials,
Hermite interpolation,
Hermite normal form,
Hermitian operators,
and
cubic Hermite splines
are named in his honor. One of his students was
Henri Poincare.
In 1873,
Hermite was the first to prove that
e, the base of
natural logarithms,
is a
transcendental number.
His methods were later used by
Ferdinand von Lindemann
to prove
in 1882
π is transcendental.
In a letter to
Thomas Stieltjes in
1893, Hermite famously remarked: "I turn with terror and horror from this
lamentable scourge of
continuous functions with no derivatives."
See
http://www.pi314.net/eng/lindemann.php
Leopold
Kronecker (1823
– 1891):
(German) He
worked on number theory and algebra. He criticized Cantor's
work on
set
theory,
and was quoted by Weber
(1893) as
having said, "Die ganzen Zahlen hat der
liebe Gott gemacht, alles andere ist Menschenwerk" ("God made the integers, all else is the
work of man.").
Kronecker
was a student and lifelong friend of Ernst
Kummer.
For several years Kronecker
focused on business, and although he continued to study mathematics as a
hobby and corresponded with Kummer, he published no mathematical results. For
several years Kronecker focused on business, and although he continued to
study mathematics as a hobby and corresponded with Kummer, he published no
mathematical results. In 1853 he wrote a memoir on the algebraic
solvability of equations extending the work of Évariste
Galois on
the theory
of equations.
Bernhard Riemann (1826-1866): If the
"Riemann Hypothesis"
is true, the exact number of primes less than a given number N, or
Pi(N), can be calculated exactly. Although thought to be
correct, this hypothesis is unproven. Karl Friedrich
Gauss (1777-1855) had an approximation to Pi(N), equal to N/ln(N),
where ln is the natural logarithm. Adrien-Marie Legendre
(1752-1833)
improved on Gauss's estimate using Pi(N) = N/{ln(N) - 1.08366}
Gauss then improved upon that estimate using Li(N) , which he
called the logarithmic integral. (not shown here) Leonard Euler
(1707-1783)
showed that the Riemann Zeta Function: Z(s) = The
sum of 1/n raised to the s power for n = 1 to infinity, is also
equal to a product series involving primes. Z(s) = The product
of (1 + 1/p to the s + 1/p to the 2s + 1/p to the 3s + 1/p to the 4s +
1/p to the 5s +...) over all primes. It is important to note:
"s" is a "complex number". Riemann then hypothesized that Z(s) = 0 for only
complex numbers where the real part = 1/2. The Riemann Hypothesis has
not been proven, but computers have shown the first 6.3 billion zeros all
lie on the line s = 1/2 +ki. If the Riemann Hypothesis is correct,
then Riemann has a formula for calculating Pi(N) exactly!
Pi(N) = R(N) minus an Adjustment. R(N) is a formula involving
the logarithmic integral and the Adjustment is expressed in terms of the
zeros of the Zeta Function. The function R(N) was named in honor of Riemann.
The Riemann zeta function ζ(s) is a function of a
complex variable s = σ + it. (The notation with s,
σ, and t is traditionally used in the study of the ζ-function)
The following
infinite series converges for all complex numbers s with real
part greater than 1, and defines ζ(s) in this case:
-
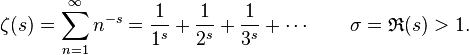
The Riemann zeta function is defined as the
analytic continuation of the function defined for σ > 1 by the sum of
the preceding series. When s =2 , this function equals
Riemann's hypothesis in 1859 is a deep mathematical conjecture which
states that the nontrivial
Riemann
zeta function zeros, i.e., the values of
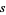other than
 ,
 ,
 ,
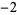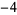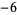... such that
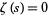(where
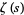is the
Riemann zeta function) all lie on the "critical
line"
![sigma=R[s]=1/2](http://mathworld.wolfram.com/images/equations/RiemannHypothesis/Inline7.gif)
(where
![R[s]](http://mathworld.wolfram.com/images/equations/RiemannHypothesis/Inline8.gif)
denotes the real part
of
 ).
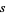It has never been proved or disproved.
| Riemann zeta function ζ(s) in the
complex plane. The color of a point s encodes the value of
ζ(s): colors close to black denote values close to zero,
while hue
encodes the value's
argument. The white spot at s = 1 is the pole of the zeta
function; the black spots on the negative real axis and on the critical
line Re(s) = 1/2 are its zeros. Values with arguments close to
zero including positive reals on the real half-line are presented in
red. |
 |
Julius Wilhelm Richard Dedekind
(1831-1916): (
German) He did
important work in
abstract algebra
(particularly
ring theory),
algebraic number theory
and the foundations of the
real numbers.
James Clerk Maxwell (1831-1879): (Scottish)
A physicist and mathematician.
His most prominent achievement was formulating classical
electromagnetic theory.
This united all previously unrelated observations, experiments and equations
of electricity, magnetism and even optics into a consistent theory.
Maxwell's equations
demonstrated that electricity, magnetism and even light are all
manifestations of the same phenomenon, namely the
electromagnetic field.
Subsequently, all other classic laws or equations of these disciplines
became simplified cases of Maxwell's equations. Maxwell's achievements
concerning electromagnetism have been called the "second great unification
in physics", after the first one realised by
Isaac Newton.
Maxwell demonstrated that
electric and
magnetic fields
travel through space in the form of
waves, and at the
constant
speed of light. In
1864 Maxwell wrote
A Dynamical Theory of the Electromagnetic Field.
It was with this that he first proposed that
light was in fact
undulations in the same medium that is the cause of electric and magnetic
phenomena. His work in producing a unified
model of
electromagnetism is
one of the greatest advances in physics.
Georg Ferdinand Ludwig Philipp Cantor
(1845-1918): (German)
He is best known as the inventor of
set theory, which has
become a
fundamental theory in
mathematics. Cantor established the importance of
one-to-one correspondence
between sets, defined
infinite and
well-ordered sets,
and proved that the
real numbers are
"more numerous" than the
natural numbers. In
fact,
Cantor's theorem
implies the existence of an "infinity
of infinities". He defined the
cardinal and
ordinal numbers and
their arithmetic. Cantor's work is of great philosophical interest, a fact
of which he was well aware. Cantor's theory of
transfinite numbers
was originally regarded as so counter-intuitive, even shocking, that it
encountered
resistance from
mathematical contemporaries such as
Leopold Kronecker and
Henri Poincare
and later from
Hermann Weyl and
L. E. J. Brouwer.
A transcendental number is a (possibly
complex) number that is not
algebraic—that is, it is not a
root of a non-zero
polynomial equation with
rational
coefficients. The most prominent examples
of transcendental numbers are
π
and
e. Though only a few classes of
transcendental numbers are known (in part because it can be extremely
difficult to show that a given number is transcendental), transcendental
numbers are not rare. Indeed,
almost all
real and complex
numbers are transcendental, since the algebraic numbers are
countable while the
sets of real and complex numbers are both
uncountable.
All real transcendental numbers are
irrational, since all rational numbers are
algebraic. The
converse is not true: not all irrational
numbers are transcendental; e.g., the
square root of 2 is irrational but not a
transcendental number, since it is a solution of the polynomial equation
x2 − 2 = 0.
Seth Carlo Chandler, Jr. (1846-1913):
(American
astronomer and actuary).
He was born in
Boston,
Massachusetts to Seth Carlo and Mary (née
Cheever) Chandler.During his last year in high school he performed
mathematical computations for
Benjamin Peirce, of the
Harvard College Observatory.
After graduating, he
became the assistant of
Benjamin A. Gould. Gould was director of
the Longitude Department of the
U.S. Coast Survey program, a
geodetic survey program. When Gould left to
become director of the national observatory in
Argentina, Chandler also left and became
an actuary for Continental Life in NY City. However, he
continued to work in astronomy as an amateur affiliated with Harvard College
Observatory.
In 1876 Chandler
moved his family to Boston where he continued his actuarial work as a
consultant to Union Mutual Life Insurance Company. In 1880 he renewed
his association with the Harvard College Observatory. In 1881 he moved
to Cambridge. He mounted a telescope to the cupola atop the roof
and carried on the duties of Associate Editor of the Astronomical Journal
while B. A. Gould was editor. He later became editor and used his own
funds to publish this journal in difficult financial times.
Chandler is best known for his discovery (1884–85) of the
Chandler Wobble, a
movement in
Earth’s axis of rotation that causes
latitude to vary with a period of
about 433 days. A wandering of the rotation axis had been predicted by Swiss
mathematician
Leonhard Euler in 1765. Chandler’s
detection of this effect was facilitated by his invention of the
almucantar, a device for measuring
the positions of
stars relative to a circle centered
at the
zenith rather than to the
meridian. The
North Pole of Earth’s rotation axis
wanders in an irregular, quasi-circular path with a radius of about 8–10
metres (26–33 feet).
From 1896 to 1909 he edited The Astronomical Journal.
Chandler also made contributions to other areas of astronomy, including
variable stars. He independently
co-discovered the
nova
T Coronae Borealis, improved the estimate
of the
constant of aberration, and computed the
orbital parameters of
asteroids and
comets.
Chandler was awarded the
Gold Medal of the Royal Astronomical Society
in 1896 and the
James Craig Watson Medal in 1894. The
crater
Chandler on the
Moon is named after him.
See his bio at:
http://www.nasonline.org/publications/biographical-memoirs/memoir-pdfs/chandler-seth-c.pdf
See more on the Chandler Wobble:
http://curiosity.discovery.com/question/what-is-the-chandler-wobble
Thomas Alva Edison (1847-1931):
(American) An inventor, scientist, and
businessman who developed many devices that greatly influenced life around
the world, including the
phonograph, the
motion picture camera,
and a long-lasting, practical electric
light bulb. Dubbed
"The Wizard of Menlo Park" . He was born in
Milan, Ohio. His quotations include:
"There's a way to do it better - find it!"
"Genius is one percent inspiration and ninety-nine percent perspiration."
"I have not failed. I've just found 10,000 ways that won't work." "I
never did a day's work in my life. It was all fun." Also:
"We will make electricity so cheap that only the rich will burn candles." Edison
became the owner of his Milan, Ohio, birthplace in 1906. On his last visit,
in 1923, he was shocked to find his old home still lit by lamps and candles.
Al Bolisha, a Canadian humorist, said, "Do you realize if it weren't for
Edison, we'd be watching TV by candelight?"
Prime Number Theorem states that if you
select a large number N, the probability of it being prime is about
1/Ln(N) was solved independently in 1896 by Jacques-Solomon
Hadamard (1865-1963) and
Charles de la Vallee Poisson (1866-1962) by showing that the Riemann
Zeta Function has no zeros of the form (1 + ki).
Carl Louis Ferdinand von Lindemann (1852-1939):
(German) He was a noted for his proof, published in 1882,
that π (pi) is a
transcendental number,
i.e., it is not a zero of any
polynomial with
rational
coefficients.
Jules Henri Poincare (1854-1912):
(French) A mathematician, theoretical physicist, and a philosopher of
science. Poincare is often described in mathematics as The
Last Universalist, since he excelled in all fields of the discipline as
it existed during his lifetime.
George Eastman (1854-1932):
(American) An inventor and
philanthropist. He
founded the
Eastman Kodak Company
and invented
roll film
In his final two years, Eastman was in intense pain, caused by a
degenerative disorder affecting his spine. He had trouble standing and his
walking became a slow shuffle. Today it might be diagnosed as
lumbar spinal stenosis,
a narrowing of the spinal canal caused by
calcification in the
vertebrae. Eastman grew depressed, as he had seen his mother spend the last
two years of her life in a wheelchair from the same condition. On
March 14, 1932, Eastman died by suicide with a single gunshot to the heart,
leaving a note which read, "My work is done. Why wait?"
 |
The logo from 1987 to 2006. The letter "K" had
been a favorite of Eastman's, he is quoted as saying, "it seems a
strong, incisive sort of letter." He and his mother devised the name
Kodak with an anagram set. He said that there were three principal
concepts he used in creating the name: it should be short, one cannot
mispronounce it, and it could not resemble anything or be associated
with anything but Kodak. |
Andrey (Andrei) Andreyevich Markov (Андрей
Андреевич Марков) (1856-1922): (Russian) He is best
known for his work on theory of
stochastic processes.
His research later became known as
Markov chains.
Henry Ernest Dudeney (1857-1930):
(English) An author and mathematician who specialized in logic puzzles and
mathematical games. He is known as one of the foremost creators of puzzles.
Max Karl Ernst Ludwig Planck (1858-1947):
(German) A
physicist who is
regarded as the founder of the
quantum theory, for
which he received the
Nobel Prize in Physics
in 1918.
David Hilbert (1862-1943): (German) He was recognized as
one of the most influential and universal mathematicians of the 19th and
early 20th centuries. He discovered and developed a broad range of
fundamental ideas in many areas,
including
invariant theory and
the
axiomatization of geometry.
He also formulated the theory of
Hilbert spaces, one
of the foundations of
functional analysis.
Bertrand Russell (1872-1970): "Physics is mathematical not
because we know so much about the physical world, but because we know so
little; it is only its mathematical properties we can discover."
Pierre Joseph Louis Fatou (1878 – 1929):
(French): He was a French mathematician and
astronomer. He is known for major
contributions to several branches of
analysis. The
Fatou lemma and the
Fatou set are named after him.
Albert Einstein (1879-1955): The speed of light is the
same, irrespective of how the source of light or the observer is moving.
Furthermore, space and time cannot be treated as separate entities, rather
they are inseparably tethered together by
symmetry. One of the known results of special relativity is that
the length of moving bodies, as measured by observers at rest, contracts
along their direction of motion. The contraction is larger, the
higher the speed. Gravity warps and bends spacetime. One of the key
predictions of general relativity was the bending of light rays under the
influence of gravity. Guided by
principles of symmetry Einstein showed that acceleration and gravity
are two sides of the same coin.(If a train is moving very fast to the north
and a man in a boxcar drops his keys, they fall to the south.)(If a man in a
stationary box car drops his keys, the keys would fall to the south, if
gravity was tilted to the south.)
Amalie Emmy Noether (1882-1935): (German)
A
German
mathematician known
for her groundbreaking contributions to
abstract algebra and
theoretical physics.
Described by
Pavel Alexandrov,
Albert Einstein,
Jean Dieudonné,
Hermann Weyl,
Norbert Wiener and
others as the most important woman in the history of mathematics,
she revolutionized the theories of
rings,
fields, and
algebras. In physics,
Noether's theorem
explains the fundamental connection between
symmetry and
conservation laws.
Max Born (1882-1970): (German)
A
physicist and
mathematician who was
instrumental in the development of
quantum mechanics. He
also made contributions to
solid-state physics
and
optics and supervised
the work of a number of notable physicists in the 1920s and 30s. Born won
the 1954
Nobel Prize in Physics,
shared with
Walther Bothe.
Frank Albert Benford, Jr. (1883-1948):
(American) Benford's law, also called the
first-digit law, states that in lists of numbers from many (but not
all) real-life sources of
data, the leading
digit is distributed in a specific, non-uniform way. According to this law,
the first digit is 1 almost one
third of the time,
and larger digits occur as the leading digit with lower and lower frequency,
to the point where 9 as a first digit occurs less than one time in twenty.
This distribution of first digits arises logically whenever a set of values
is distributed
logarithmically.
Measurements of real world values are often distributed logarithmically (or
equivalently, the logarithm of the measurements is distributed uniformly).
This counter-intuitive result has been found to apply to a wide
variety of data sets, including electricity bills,
street addresses, stock prices, population numbers, death rates, lengths of
rivers,
physical and
mathematical constants,
and processes described by
power laws (which are
very common in nature). The result holds regardless of the
base in which the
numbers are expressed, although the exact proportions change. It is named
after physicist
Frank Benford, who
stated it in 1938, although it had been previously stated by
Simon Newcomb in
1881.
John Maynard Keynes
(1883-1946):
British Economist and Mathematician. On the Law of Large Numbers
or "long run calculations", he said: "This long run is a misleading guide to
current affairs. In the long run we are all dead.
Economists set themselves too easy, too useless a task if in tempestuous
seasons they can only tell us that when the storm is long past the ocean is
flat again." Other quotes: "I do not know which makes a man more
conservative - to know nothing but the present, or nothing but the past."
" It would be foolish, in forming our expectations, to attach great weight
to matters which are very uncertain." " It is generally agreed that
casinos should, in the public interest, be inaccessible and expensive. And
perhaps the same is true of Stock Exchanges." "The outstanding faults
of the economic society in which we live are its failure to provide for full
employment and its arbitrary and inequitable distribution of wealth and
incomes."
Niels Henrik David Bohr (1885-1962):
(Danish) A
physicist who made
fundamental contributions to understanding
atomic structure and
quantum mechanics,
for which he received the
Nobel Prize in
Physics in 1922. Bohr
mentored and collaborated with many of the top physicists of the century at
his institute in
Copenhagen. He was
part of a team of physicists working on the
Manhattan Project.
Bohr married Margrethe Norlund in 1912, and one of their sons,
Aage Bohr, grew up to
be an important physicist who in 1975 also received the Nobel prize. Bohr
has been described as one of the most influential scientists of the 20th
century.
Srīnivāsa Aiyangār Rāmānujan (1887-1920):
(Indian) He was a
self taught
genius, with almost
no formal training in
pure mathematics,
made substantial contributions to
mathematical analysis,
number theory,
infinite series and
continued fractions.
Ramanujan's talent was said, by the prominent English mathematician
G.H. Hardy, to be in
the same league as legendary mathematicians such as
Euler,
Gauss,
Newton and
Archimedes.
Gaston Maurice Julia (1893 – 1978):
(French) He was a French mathematician who devised the formula for the
Julia set. His works were popularized
by French mathematician
Benoit Mandelbrot; the Julia and
Mandelbrot
fractals are closely related.
Enrico Fermi (1901-1954):
(Italian-American)
A
physicist
particularly known for his work on the development of the first
nuclear reactor,
Chicago Pile-1, and
for his contributions to the development of
quantum theory,
nuclear and
particle physics, and
statistical mechanics.
He was awarded the 1938
Nobel Prize in Physics
for his work on
induced radioactivity.
Fermi is widely regarded as one of the leading
scientists of the
20th century, highly
accomplished in both theory and experiment.
Along with
J. Robert Oppenheimer,
he is frequently referred to as "the father of the
atomic bomb".
He also held
several patents
related to the use of nuclear power.
Andre John von Neumann
(1903-1957): (Hungarian-born)
An
American
mathematician who
made major contributions to a vast range of fields, including
set theory,
functional analysis,
quantum mechanics,
ergodic theory,
continuous geometry,
economics and
game theory,
computer science,
numerical analysis,
hydrodynamics (of
explosions), and
statistics, as well
as many other mathematical fields. He is generally regarded as one of the
greatest mathematicians in modern history. The mathematician
Jean Dieudonne called
von Neumann "the last of the great mathematicians",while
Peter Lax described
him as possessing the most "fearsome technical prowess" and "scintillating
intellect" of the century.Weil (1906-1998): (from
France) "God exists since mathematics is consistent, and the Devil exists
since we cannot prove it."
Julius Robert Oppenheimer (1904-1967):
(American) A
theoretical physicist
and professor of physics at the
University of California, Berkeley.
He is often called the "father of the atomic bomb" for his role as
the scientific director of the
Manhattan Project,
the
World War II project
that developed the first
nuclear weapons. The
first atomic bomb was detonated in July 1945 in the
Trinity test in
New Mexico;
Oppenheimer remarked later that it brought to mind words from the
Bhagavad Gita: "Now,
I am become Death, the destroyer of worlds."
After the war he became a chief adviser to the
newly created
United States Atomic Energy Commission
and used that position to lobby for international control of
nuclear power to
avert
nuclear proliferation
and an
arms race with the
Soviet Union. After provoking the ire of many politicians with his outspoken
opinions during the
Second Red Scare, he
had his
security clearance
revoked in a much-publicized hearing in 1954. Though stripped of his direct
political influence he continued to lecture, write and work in physics. A
decade later President
John F. Kennedy
awarded (and
Lyndon B. Johnson
presented) him with the
Enrico Fermi Award as
a gesture of
political rehabilitation.
Oppenheimer's notable achievements in physics
include the
Born Oppenheimer approximation
for molecular
wavefunctions, work
on the theory of
electrons and
positrons, the
Oppenheimer Phillips process
in
nuclear fusion, and
the first prediction of
quantum tunneling.
With his students he also made important contributions to the modern theory
of
neutron stars and
black holes, as well
as to
quantum mechanics,
quantum field theory,
and the interactions of
cosmic rays. As a
teacher and promoter of science, he is remembered as a founding father of
the American school of theoretical physics that gained world prominence in
the 1930s. After World War II, he became director of the
Institute for Advanced Study
in Princeton.
Kurt Goedel (1906-1978): (Austrian and later
American) A logician, mathematician,
and philosopher.
Considered with Aristotle and Gottlob
Frege to be one of the
most significant logicians in history) Goedel's Incompleteness Theorem: Any
consistent axiom system is necessarily incomplete in that there will be true
statements that can't be deduced from the axioms.
Gödel published his two incompleteness
theorems in
1931 when he was 25 years old, one year after finishing his doctorate at the University
of Vienna. The first
incompleteness theorem states that for any self-consistent recursive axiomatic
system powerful
enough to describe the arithmetic of the natural
numbers (for
example
Peano arithmetic),
there are true propositions about the naturals that cannot be proved from
the axioms.
To prove this theorem, Gödel developed a technique now known as Gödel
numbering, which codes formal
expressions as natural numbers.
He also showed that neither the axiom
of choice nor
the continuum
hypothesis can
be disproved from the accepted axioms
of set theory, assuming these
axioms are consistent. The former result opened the door for mathematicians
to assume the axiom of choice in their proofs. He also made important
contributions to proof
theory by
clarifying the connections between classical
logic, intuitionistic
logic, and modal
logic.
Olga Taussky-Todd
(1906
– 1995):
(Austrian and
later Czech-American)
She was born into a Jewish
family. She worked first in
algebraic
number theory, with a
doctorate at the University
of Vienna supervised
by Philipp
Furtwängler. During
that time in Vienna she also attended the meetings of the Vienna
Circle.
According to Gian-Carlo
Rota, as a young mathematician
she was hired by a group of German mathematicians to find and correct the
many mathematical errors in the works of David
Hilbert, so that they could be
collected into a volume to be presented to him on his birthday. There was
only one paper, on the continuum
hypothesis,
that she was unable to repair.
Later, she started to use matrices to
analyze vibrations of airplanes during World
War II, at the National
Physical Laboratory in
the United
Kingdom. She became the
torchbearer for matrix
theory. In 1935, she moved to
England and became a Fellow at Girton
College, Cambridge University,
as well as at Bryn
Mawr College. In 1938 she
married the British mathematician John
Todd (1911-2007),
a colleague at the University
of London. In 1945 the
Todds emigrated to the United States and worked for the National
Bureau of Standards. In 1957
they joined the faculty of California
Institute of Technology
(Caltech) in Pasadena, California.
Andre Weil
(1906-1998): (French)
He was an influential
mathematician of the
20th century, renowned for the breadth and quality of his research output,
its influence on future work, and the elegance of his exposition. He is
especially known for his foundational work in
number theory and
algebraic geometry
James R Newman (1907-1966): (American) Von Neumann's
first significant contribution to economics was the minimax theorem in1928.
He eventually improved and extended the minimax theorem to include games
involving imperfect information and games with more than two players. This
work culminated in the 1944 classic
Theory of Games and Economic Behavior.
Von Neumann was one of the pioneers of computer science making significant
contributions to the development of logical design. "The Theory of
Groups is a branch of mathematics in which one does something to
something and then compares the result with the result obtained
from doing the same thing to something else, or something else to the same
thing."
Edward Teller (1908-2003):
(Hungarian-born
American) A
theoretical
physicist, known
colloquially as "the father of the
hydrogen bomb,"
even though he did not care for the title. In 1942, Teller was
invited to be part of
Robert Oppenheimer's
summer planning seminar at the
University of California, Berkeley
for the origins of the
Manhattan Project,
the
Allied effort to
develop the first
nuclear weapons. A
few weeks earlier, Teller had been meeting with his friend and colleague
Enrico Fermi about
the prospects of
atomic warfare, and
Fermi had nonchalantly suggested that perhaps a weapon based on
nuclear fission could
be used to set off an even larger
nuclear fusion
reaction. Even though he initially explained to Fermi why he thought the
idea would not work, Teller was fascinated by the possibility and was
quickly bored with the idea of "just" an atomic bomb (even though this was
not yet anywhere near completion). At the Berkeley session, Teller diverted
discussion from the fission weapon to the possibility of a fusion weapon,
what he called the "Super" (an early version of what was later known as a
hydrogen bomb).
Stanislaw Marcin Ulam
(1909-1984): (Polish-Jewish) He
participated in America's
Manhattan Project,
originated the
Teller–Ulam design of
thermonuclear weapons,
invented the
Monte Carlo method of computation,
and suggested
nuclear pulse propulsion.
In pure and applied mathematics, he produced many results, proved many
theorems, and proposed several conjectures.
Alan Turing 1912-1954): A British
mathematician,
logician,
cryptanalyst and
computer scientist.
He was highly influential in the development of
computer science,
giving a formalisation of the concepts of "algorithm"
and "computation"
with the
Turing machine, which
can be considered a model of a general purpose computer.
Turing is widely considered to be the
father of theoretical
computer science and
artificial intelligence.
During
World War II, Turing
worked for the
Government Code and Cypher School (GC&CS)
at
Bletchley Park,
Britain's
code breaking centre.
For a time he led
Hut 8, the section
responsible for German naval cryptanalysis. He devised a number of
techniques for breaking German
ciphers, including
the
bombe method, an
electromechanical
machine that could find settings for the
Enigma machine.
His algorithms used Bayes Theorem.
Turing had something of a reputation for
eccentricity at Bletchley Park. He was known to his colleagues as 'Prof' and
his treatise on Enigma was known as 'The Prof's Book'.
Jack Good, a
cryptanalyst who worked with him, is quoted by
Ronald Lewin as
having said of Turing:
In the first week of June each year he would get
a bad attack of hay fever, and he would cycle to the office wearing a
service gas mask to keep the pollen off. His bicycle had a fault: the
chain would come off at regular intervals. Instead of having it mended
he would count the number of times the pedals went round and would get
off the bicycle in time to adjust the chain by hand. Another of his
eccentricities is that he chained his mug to the radiator pipes to
prevent it being stolen.
While working at Bletchley, Turing, a talented
long-distance runner, occasionally ran the 40 miles (64 km) to London when
he was needed for high-level meetings, and he was capable of world-class
marathon standards.
Turing was prosecuted for
homosexual acts in 1952, when such acts
were still
criminalised in the UK. He accepted being
chemically castrated as an alternative to prison. He died in 1954, 42 days
before his 42nd birthday from cyanide poison ing. An inquest
determined his death a suicide, his mother and some others believe it
was accidental. See
http://www.cbsnews.com/news/wwii-codebreaker-alan-turing-gets-royal-pardon-for-gay-conviction/
There were prominent
mathematicians that did not embrace the logic of Bayes Theorem. Alan
Turing used it to decode the German Enigma Cipher.
http://lesswrong.com/lw/774/a_history_of_bayes_theorem/
Turing worked from 1952 until his
death in 1954 on mathematical biology, specifically morphogenisis.
He published one paper on the subject called The Chemical Basis of
Morphogenesis in 1952, putting forth the Turing hypothesis of pattern
formation (the theory was experimentally confirmed 60 years after his
death). His central interest in the field was understanding
Fibonacci phyllotaxis, the existence of Fibonacci numbers in plant
structures. He used reaction-diffusion equations which are central to the
field of pattern formation. Later papers went unpublished until 1992
when Collected Works of A. M. Turing was published. His contribution
is considered a seminal piece of work in this field. Removal of Hox genes
causes an increased number of digits (up to 14) in mice, demonstrating a
Turing-type mechanism in the development of the hand.
Paul Erdős (1913-1996): (from
Budapest, Hungary) Erdős published more papers than any other
mathematician in history, working with hundreds of collaborators. His
colleague
Alfred Renyi said, "a mathematician is a
machine for turning coffee into theorems", and Erdős drank copious
quantities.
Because of his prolific output, friends created the
Erdős number
as a humorous tribute; Erdős alone was assigned the Erdős number of 0 (for
being himself), while his immediate collaborators could claim an Erdős
number of 1, their collaborators have Erdős number at most 2, and so on.
Approximately 200,000 mathematicians have an assigned Erdős number, and some
have estimated that 90 percent of the world's active mathematicians have an
Erdős number smaller than 8.
It is said that Hank Aaron has an Erdős number of 1 because they
both autographed the same baseball when
Emory University awarded them honorary
degrees on the same day. Erdős numbers have also been assigned to an infant,
a horse, and several actors.
Martin Gardner (1914-2010): (American) A mathematics
and science writer specializing in recreational mathematics, but with many
interests (especially the writings of Lewis Carroll. He wrote the
Mathematical Games column in Scientific American from 1956 to 1981, the
Notes of a Fringe-Watcher
column in Skeptical Inquirer from 1983 to 2002, and published over 70 books.
See:
http://en.wikipedia.org/wiki/Martin_Gardner
Ivan Niven (1915-1999):
(Canadian) Ivan published over sixty papers, some with well-known
co-authors such as Samuel Eilenberg, Paul Erdos (6 times), Nathan J. Fine,
R. D. James, and H. S. Zuckerman (7 times). His areas of expertise were
number theory, especially the areas of diophantine approximation and
questions of irrationality and transcendance of numbers, and combinatorics.
Ken Ross found two of the articles of special interest: his famous 1947
paper containing a simple proof that pi is irrational and his 1969 Monthly
article on formal power series, for which he received the Lester R. Ford
Award. Ivan viewed his most significant paper to be, "Uniform distribution
of sequences of integers".
Richard Feynman
(1918-1988):
Feynman said: "Mathematics is looking for patterns".
"Mathematics is only patterns". "Nature uses only
the longest threads to weave her patterns, so that each small piece of her
fabric reveals the organization of the entire tapestry." Also:
"Physics is like sex. Sure, it may give some practical results, but
that's not why we do it".
Murray Gell-Mann commented to the New York Times that the
Feynman Algorithm to solve a problem is:
1. Write down the problem
2. Think very hard
3. Write down the answer.
Benoit Mandelbrot (1924- 2010):
(from France) The Father of Fractal Geometry. He was a
Polish-born, French and American
mathematician, noted for developing a
"theory of roughness" in nature and the field of
fractal geometry to help prove it,
which included coining the word "fractal". He later discovered the
Mandelbrot set of intricate,
never-ending fractal shapes, named in his honor.
While he was a child, his family fled to France in 1936 to escape
the growing Nazi persecution of Jews. From 1945 to 1947 attended the
École Polytechnique, where he studied under
Gaston Julia and
Paul Lévy. From 1947 to 1949 he studied at
California Institute of Technology, where
he earned a master's degree in
aeronautics. Returning to France, he
obtained his
PhD degree in Mathematical Sciences at the
University of Paris in 1952.
In 1945 Mandelbrot's uncle had introduced him to
Julia's important 1918 paper claiming that it was a masterpiece and a
potential source of interesting problems, but Mandelbrot did not like it.
Indeed he reacted rather badly against suggestions posed by his uncle since
he felt that his whole attitude to mathematics was so different from that of
his uncle. Instead Mandelbrot chose his own very different course which,
however, brought him back to
Julia's paper in the 1970s after a path through many different sciences
which some characterize as highly individualistic or nomadic. In fact the
decision by Mandelbrot to make contributions to many different branches of
science was a very deliberate one taken at a young age. It is remarkable how
he was able to fulfill this ambition with such remarkable success in so many
areas.
As a visiting professor at
Harvard University, Mandelbrot began to
study fractals called
Julia sets that were invariant under
certain transformations of the
complex plane. Building on previous work by
Gaston Julia and
Pierre Fatou, Mandelbrot used a
computer to plot images of the Julia sets. While investigating the topology
of these Julia sets, he studied the
Mandelbrot set fractal that is now named
after him.
With the aid of computer graphics, Mandelbrot who then
worked at IBM's Watson Research Center, was able to show how
Julia's work is a source of some of the most beautiful fractals known
today. To do this he had to develop not only new mathematical ideas, but
also he had to develop some of the first computer programs to print
graphics. See his bio at
http://www-history.mcs.st-and.ac.uk/Biographies/Mandelbrot.html
There are many beautiful pictures to view on the web. For example:
http://sprott.physics.wisc.edu/fractals.htm
Also there are terrific videos to be found at:
http://www.fractal-animation.net/ufvp.html and
http://www.ericbigas.com/fractalanimation/index.html and
http://www.fractal-animation.net/ufvp.html and
http://fractalanimations.com/
and
http://www.google.com/images?hl=&q=fractal+animation&rlz=1B3GGLL_enUS405US405&um=1&ie=UTF-8&source=univ&ei=2-dFTfmfPI-p8AaSw42EAg&sa=X&oi=image_result_group&ct=title&resnum=6&ved=0CEoQsAQwBQ&biw=1045&bih=404
and
http://video.google.com/videoplay?docid=1619313842463920970#docid=8570098277666323857
and
http://video.google.com/videoplay?docid=1619313842463920970#docid=6460130356432628677
and
http://www.youtube.com/watch?v=34zPvmNXTYQ and
http://www.youtube.com/watch?v=G_GBwuYuOOs .
Learn from Robert Devaney at:
http://video.google.com/videoplay?docid=1619313842463920970#docid=-6460544449138143366
Fractal art is shown at:
http://www.lifesmith.com/art2008.html and at
http://www.lifesmith.com/art2006.html and
http://www.lifesmith.com/art2007.html
I presented some pictures of fractals and some background at the Annual
Meeting of the Society of Actuaries when I was president in 1992. I may have
used
Robert Devaney to develop the script. See
Chaos video, but start about 40% of the way through. (OOPs is copywrite
protected so will only play on my computer)
Alexander Grothendieck (1928--2014):
(German) He is one of the most influential
mathematicians of the 20th century. He
is known principally for his revolutionary advances in
algebraic geometry, and also for major
contributions to
number theory,
category theory and
homological algebra, and his early
achievements in
functional analysis. He was awarded the
Fields Medal in 1966.
He became the leading figure in the creation of modern algebraic geometry.
His research extended the
scope of the field and added elements of commutative algebra,
homological algebra, sheaf theory and category theory to its foundations,
while his so-called "relative" perspective
led to revolutionary advances in many areas
of pure
mathematics. Murray Gell-Mann (1929-
): (American) A
physicist and
polymath who received
the 1969
Nobel Prize in physics
for his work on the theory of
elementary particles.
He is a Distinguished Fellow and co-founder of the
Santa Fe Institute
and the Presidential Professor of Physics and Medicine at the
University of Southern California.
He formulated the
quark model of
hadronic resonances, and identified the SU(3)
flavor symmetry of
the light quarks, extending
isospin to include
strangeness, which he
also discovered. He developed the V-A theory of the
weak interaction in
collaboration with
Richard Feynman. He
created
current algebra in
the 1960s as a way of extracting predictions from quark models when the
fundamental theory was still murky, which led to model-independent
sum rules confirmed
by experiment.
Roger Penrose (1931 -
): (British) A mathematician and physicist .
www.en.wikipedia.org/wiki/Roger_Penrose
Robert
Phelan Langlands (1936 - ): (Canadian)
He is best known as the founder of the Langlands
Program, a vast web of
conjectures and results connecting representation
theory and automorphic
forms to the study of Galois
groups in number
theory. He is an emeritus professor and
occupies Albert
Einstein's office at the Institute
for Advanced Study in
Princeton.
See
projects.thestar.com/math-the-canadian-who-reinvented-mathematics/ and
www.math.ubc.ca/Dept/Newsletters/Robert_Langlands_interview_2010.pdf
and
www.math.duke.edu/langlands/
and Frenkel's discription:
https://math.berkeley.edu/~frenkel/review.pdf
Also, Frenkel writes:
The Langlands Program was launched in the late 60s with the goal of relating
Galois representations and automorphic forms. In recent years a geometric
version has been developed which leads to a mysterious duality between
certain categories of sheaves on moduli spaces of (flat) bundles on
algebraic curves. Three years ago, in a groundbreaking advance, Kapustin and
Witten have linked the geometric Langlands correspondence to the S-duality
of 4D supersymmetric gauge theories. This and subsequent works have already
led to striking new insights into the geometric Langlands Program, which in
particular involve the Homological Mirror Symmetry of the Hitchin moduli
spaces of Higgs bundles on algebraic curves associated to two Langlands dual
Lie groups.
Langlands Program
A grand unified theory of mathematics which includes the
search for a generalization of Artin
reciprocity (known
as Langlands reciprocity) to non-Abelian Galois extensions of number
fields. In a January 1967 letter to André
Weil, Langlands proposed that the mathematics of algebra (Galois
representations) and analysis (automorphic
forms) are intimately related, and that
congruences over finite
fields are
related to infinite-dimensional representation theory. In particular,
Langlands conjectured that the transformations behind general reciprocity
laws could be represented by means of matrices (Mackenzie
2000).
In 1998, three mathematicians proved Langlands'
conjectures for local
fields, and in a November 1999 lecture at the
Institute for Advanced Study at Princeton University, L. Lafforgue presented
a proof of the conjectures for function
fields. This leaves only the case of number
fields as
unresolved (Mackenzie 2000).
www.ams.org/journals/bull/1984-10-02/S0273-0979-1984-15237-6/S0273-0979-1984-15237-6.pdf
Stephen Hawkings (1942-
): (British) A physicist from Cambridge wrote "A Brief History
of Time". In it he tells the story of a lady commenting on a statement
made in a lecture on astronomy. She said: "Rubbish, The world is
really a flat plate supported on the back of a giant tortoise" When
asked what the tortoise was sitting on, her answer would have made Goedel
smile: "You're very clever, young man, very clever. But its turtles
all the way down."
Hawking is an English theoretical physicist, cosmologist, auhor and director
of research at the center for Theoretical Cosmology within the University of
Cambridge. Hawking was the first to set forth a cosmology explained by
a union of the general theory of relativity and quantum mechantics. He
is a vigorous supporter of the many-worlds interpretation of quantum
mechanics.
Stephen Hawking has worked on the basic
laws which govern the universe.
With Roger Penrose he showed that Einstein's General Theory of Relativity
implied space and time would have a beginning in the Big Bang and an end in
black holes.
Ian Stewart (1945-
): A British mathematician. Stewart came to the
attention of the mathematics teacher. The teacher had Stewart sit
mock
A-level examinations without any
preparation along with the upper-sixth students; Stewart placed first in the
examination. This teacher arranged for Stewart to be admitted to Cambridge
on a scholarship to
Churchill College, where he obtained a BA
in mathematics. Stewart then went to the
University of Warwick for his doctorate, on
completion of which in 1969 he was offered an academic position at Warwick,
where he presently professes mathematics. He is well known for his popular
expositions of mathematics and his contributions to
catastrophe theory.
While at Warwick he edited the mathematical magazine
Manifold. He also wrote a column called
"Mathematical Recreations" for
Scientific American magazine for several
years. Stewart has published more than 140
scientific papers, including a series of
influential papers co-authored with
Jim Collins on
coupled oscillators and the symmetry of animal gaits.
He lists his recreations as science fiction, painting, guitar, keeping fish,
geology, Egyptology and snorkeling.
Persi Warren Diaconis (1945-
): He is the statistician who demonstrated that it takes the average
card player no fewer than seven shuffles to create a random order in a deck
of cards.
Marilyn vos Savant (1946-
): An
American
magazine
columnist,
author,
lecturer, and
playwright. She has
written "Ask Marilyn", a Sunday column in
Parade magazine
in which she solves puzzles and answers questions from readers on a variety
of subjects.
Her September 9, 1990 column began with a question now
called The Monty Hall problem (Suppose you are on a game show and you are
given the choice of three doors. Behind one door is a car, the
others, goats. You pick a door, say #1, and the host, who knows what's
behind the doors, opens another door, say #3, which has a goat. He says to
you: 'Do you want to pick door #2?' Is it to your advantage to switch doors?
Marilyn vos Savant answered arguing that the selection should be switched to
door #2 because it has a 2/3 chance of success, while door #1 has just 1/3.
This response provoked letters of thousands of readers, nearly all arguing
doors #1 and #2 each have an equal chance of success.
A follow-up column reaffirming her position served only to intensify the
debate and soon became a feature article on the front page of
The New York Times.
Among the ranks of dissenting arguments were hundreds of academics and
mathematicians.
In a subsequent column, vos Savant offered numerous
explanations as to why her solution is correct. She also called upon
elementary teachers to simulate the problem in their class. Numerous
elementary school math classes devoted themselves to this experiment,
playing the game hundreds of times and reporting their results. Nearly 100%
of those classes found that your odds of winning were doubled if you switch
doors.
Finally, thanks to the diligence of elementary school children, the
controversy subsided.
Dr. Keith Devlin (1947- ):
This professor from Stamford defines Mathematics as the Science of
Patterns.
Robert L. Devaney (circa 1948-
): A native of Methuen, Massachusetts, is currently Professor
of Mathematics at Boston University. He received his undergraduate degree
from the College of the Holy Cross in 1969 and his PhD from the University
of California at Berkeley in 1973 under the direction of Stephen Smale. He
taught at Northwestern University and Tufts University before coming to
Boston University in 1980. His main area of research is dynamical
systems, primarily complex analytic dynamics, but also including more
general ideas about chaotic dynamical systems. Lately, he has become
intrigued with the incredibly rich topological aspects of dynamics,
including such things as indecomposable continua, Sierpinski curves, and
Cantor bouquets.
Devaney developed the 8 minute script contained in the middle of the
presentation on Chaos
that Don had presented for the 1992 Annual Meeting of the Society of
Actuaries. This link only works on Don's computer.
Edward Witten (1951-
): One of the researchers at Princeton working on "string
theory" which may help with the clash between the central ideas of general
relativity and quantum mechanics when it comes to extremely small
scales. He is regarded by many of his peers as one of the greatest living
physicists, perhaps even a successor to
Albert Einstein.
In 1990 he was awarded a
Fields Medal
by the International Union of Mathematics, which is the highest honor in
mathematics and often regarded as the Nobel Prize equivalent for
mathematics. He is the only physicist to have received this honor.
Sir Andrew John Wiles (1953-
): (British)
A professor at Princeton University in Number Theory. He published a flawed
proof of Fermat's Last Theorem in 1993. He corrected the error in
1994.
Simon Kirwan Donaldson
(1957- ): (British)
An
English mathematician
famous for his work on the
topology of smooth
(differentiable) four-dimensional
manifolds. He is now
Royal Society research professor in Pure Mathematics and President of the
Institute for Mathematical Science at
Imperial College London.
He used the solutions to the Yang-Mills equations to discover a finger-print
which allowed him to distinguish whether two shapes were actually the same.
These finger-prints are called invariants.
Steven Strogatz ( 1959 -
): (American) He is an applied mathematics professor at Cornell.
He has written an interesting book:
The Joy of X.
Marcus Peter Francis du
Sautoy
(1965 - ):
(born in London) A Professor of Mathematics at the University of Oxford. His
academic work concerns mainly group theory and number theory. He is known
for his books popularizing mathematics. In 2001 he won the
Berwick Prize of the
London Mathematical Society,
which is awarded every two years to reward the best mathematical
research by a mathematician under forty. In March, 2006, his article
Prime Numbers Get Hitched was published on
Seed Magazine's
website.
http://seedmagazine.com/content/article/prime_numbers_get_hitched/
In it he explained how the number
42, mentioned in
The Hitchhiker's Guide to the Galaxy
as the
answer to everything,
is related to the
Riemann zeta function.
See
http://www.culturenorthernireland.org/article/2836/belfast-festival-marcus-du-sautoy
Also:
http://people.maths.ox.ac.uk/dusautoy/newleft.htm and
http://people.maths.ox.ac.uk/dusautoy/newright.htm
Grigori Yakovlevich Perelman (1966-
): (from Russia) The Millennium Prize Problems
are seven problems in mathematics that were stated by the Clay Mathematics
Institute in 2000. Currently, six of the problems remain unsolved. A
correct solution to any of the problems results in a US$1,000,000 prize
(sometimes called a Millennium Prize) being awarded by the institute.
One of the problems, the Poincare' conjecture, was solved by Perelman in
2002 He was also awarded the Fields Medal in
2006. He has not accepted either prize.
Edward Vladimirovich Frenkel
(1967 circa - ): (Russian)
A mathematician working
in representation
theory, algebraic
geometry,
and mathematical
physics.
He is a professor of mathematics at University
of California, Berkeley and
author of the bestselling book Love
and Math. As a high school
student he studied higher mathematics privately with Evgeny Evgenievich
Petrov, although his initial interest was in quantum physics rather than
mathematics. He was not admitted to Moscow
State University because
of discrimination against Jews and enrolled instead in the applied
mathematics program at the Gubkin
University of Oil and Gas.
While a student there, he attended the seminar of Israel
Gelfand and
worked with Boris
Lwowitsch Feigin (de) and Dmitry
Fuchs.
After receiving his college degree in 1989, he was first invited to Harvard
University as
a visiting professor, and a year later he enrolled as a graduate student at
Harvard He received his Ph.D. at Harvard
University in
1991, after one year of study, under the direction of Joseph
Bernstein.
He was a Junior Fellow at the Harvard
Society of Fellows from
1991 to 1994, and served as an associate professor at Harvard from 1994 to
1997. He has been a professor of mathematics at University
of California, Berkeley since
1997. Frenkel's recent work has focused on the Langlands
program and
its connections to representation
theory, integrable
systems, geometry,
and physics.
Together with Dennis
Gaitsgory and Kari
Vilonen,
he has proved the geometric Langlands conjecture for GL(n).
His joint work with Robert
Langlands and Ngô
Bảo Châu suggested
a new approach to the functoriality of automorphic representations and trace
formulas. He has also been investigating (in particular, in a joint work
with Edward
Witten)
connections between the geometric
Langlands correspondence and
dualities in quantum
field theory.
RANKING OF GREAT MATHEMATICIANS See
www.fabpedigree.com/james/mathmen.htm
FIELDS MEDAL
Fields Medal
From Wikipedia, the free encyclopedia
Jump to navigationJump
to search
The Fields Medal is a prize awarded to two, three,
or four
mathematicians under 40 years of age at the
International Congress of the
International Mathematical Union (IMU), a meeting that
takes place every four years.
The Fields Medal is widely regarded as the highest honor
a mathematician can receive, and has been described by many
as the mathematician's "Nobel
Prize".[1][2][3]
According to Academic Excellence Survey by
ARWU, Fields Medal is the top award in the field of
mathematics worldwide,[4]
and in another reputation survey conducted by IREG in
2013-14, the Fields Medal came closely after the
Abel Prize as the second most prestigious international
award in mathematics.[5][6]
The prize comes with a monetary award which, since 2006,
has been
CA$15,000.[7][8]
The name of the award is in honour of
Canadian mathematician
John Charles Fields.[9]
Fields was instrumental in establishing the award, designing
the medal itself, and funding the monetary component.[9]
The medal was first awarded in 1936 to Finnish
mathematician
Lars Ahlfors and American mathematician
Jesse Douglas, and it has been awarded every four years
since 1950. Its purpose is to give recognition and support
to younger mathematical researchers who have made major
contributions. In 2014, the
Iranian mathematician
Maryam Mirzakhani became the first woman Fields
Medallist.[10][11][12]
In all, sixty people have been awarded the Fields Medal.
The most recent group of Fields Medalists received their
awards on 1 August 2018 at the opening ceremony of the IMU
International Congress, held in
Rio de Janeiro,
Brazil.[13]
Conditions of the award[edit]
The Fields Medal is often described as the "Nobel
Prize of Mathematics" and for a long time has been
regarded as the most prestigious award in the field of
mathematics.[1][2][3]
Unlike the
Nobel Prize, however, the Fields Medal is only awarded
every four years. The Fields Medal also has an age limit: a
recipient must be under age 40 on 1 January of the year in
which the medal is awarded. This is similar to restrictions
applicable to the
Clark Medal in economics. The under-40 rule is based on
Fields' desire that "while it was in recognition of work
already done, it was at the same time intended to be an
encouragement for further achievement on the part of the
recipients and a stimulus to renewed effort on the part of
others."[14]
Moreover, an individual can only be awarded one Fields
Medal; laureates are ineligible to be awarded future medals.[15]
This is in contrast with the Nobel Prize which can be, and
has been awarded to an individual or an entity more than
once, whether in the same category (John
Bardeen and
Frederick Sanger), or in different categories (Marie
Curie and
Linus Pauling).
The monetary award is much lower than the 8,000,000
Swedish kronor (roughly 1,400,000 Canadian dollars)[16]
given with each Nobel prize as of 2014.[17]
Other major awards in mathematics, such as the
Abel Prize and the
Chern Medal, have larger monetary prizes compared to the
Fields Medal.
Fields
Medalists[edit]
| 1936 |
Oslo, Norway |
Lars Ahlfors |
University of Helsinki, Finland |
Harvard University, US |
"Awarded medal for research on covering surfaces
related to
Riemann surfaces of inverse functions of entire
and meromorphic functions. Opened up new fields of
analysis." |
|
Jesse Douglas |
Massachusetts Institute of Technology, US |
City College of New York, US |
"Did important work of the Plateau problem which
is concerned with finding minimal surfaces
connecting and determined by some fixed boundary."
|
| 1950 |
Cambridge, US |
Laurent Schwartz |
University of Nancy, France |
University of Paris VII, France |
"Developed the theory of distributions, a new
notion of generalized function motivated by the
Dirac delta-function of theoretical physics." |
|
Atle Selberg |
Institute for Advanced Study, US |
Institute for Advanced Study, US |
"Developed generalizations of the sieve methods
of Viggo Brun; achieved major results on zeros of
the Riemann zeta function; gave an elementary proof
of the prime number theorem (with P. Erdős), with a
generalization to prime numbers in an arbitrary
arithmetic progression." |
| 1954 |
Amsterdam, Netherlands |
Kunihiko Kodaira |
University of Tokyo, Japan and
Institute for Advanced Study, US[26]
|
University of Tokyo, Japan |
"Achieved major results in the theory of
harmonic integrals and numerous applications to
Kählerian and more specifically to algebraic
varieties. He demonstrated, by sheaf cohomology,
that such varieties are Hodge manifolds." |
|
Jean-Pierre Serre |
University of Nancy, France |
Collège de France, France |
"Achieved major results on the homotopy groups
of spheres, especially in his use of the method of
spectral sequences. Reformulated and extended some
of the main results of complex variable theory in
terms of sheaves." |
| 1958 |
Edinburgh, UK |
Klaus Roth |
University College London, UK |
Imperial College London, UK |
"Solved in 1955 the famous Thue-Siegel problem
concerning the approximation to algebraic numbers by
rational numbers and proved in 1952 that a sequence
with no three numbers in arithmetic progression has
zero density (a conjecture of Erdös and Turán of
1935)." |
|
René Thom |
University of Strasbourg, France |
Institut des Hautes Études Scientifiques, France |
"In 1954 invented and developed the theory of
cobordism in algebraic topology. This classification
of manifolds used homotopy theory in a fundamental
way and became a prime example of a general
cohomology theory." |
| 1962 |
Stockholm, Sweden |
Lars Hörmander |
University of Stockholm, Sweden |
Lund University, Sweden |
"Worked in partial differential equations.
Specifically, contributed to the general theory of
linear differential operators. The questions go back
to one of Hilbert's problems at the 1900 congress."
|
|
John Milnor |
Princeton University, US |
Stony Brook University, US |
"Proved that a 7-dimensional sphere can have
several differential structures; this led to the
creation of the field of differential topology."
|
| 1966 |
Moscow, USSR |
Michael Atiyah |
University of Oxford, UK |
University of Edinburgh, UK |
"Did joint work with Hirzebruch in K-theory;
proved jointly with Singer the index theorem of
elliptic operators on complex manifolds; worked in
collaboration with Bott to prove a fixed point
theorem related to the "Lefschetz formula"." |
|
Paul Joseph Cohen |
Stanford University, US |
Stanford University, US |
"Used technique called "forcing" to prove the
independence in set theory of the axiom of choice
and of the generalized continuum hypothesis. The
latter problem was the first of Hilbert's problems
of the 1900 Congress." |
|
Alexander Grothendieck |
Institut des Hautes Études Scientifiques, France
|
Centre National de la Recherche Scientifique,
France |
"Built on work of Weil and Zariski and effected
fundamental advances in algebraic geometry. He
introduced the idea of K-theory (the Grothendieck
groups and rings). Revolutionized homological
algebra in his celebrated ‘Tôhoku
paper’" |
|
Stephen Smale |
University of California, Berkeley, US |
City University of Hong Kong, Hong Kong |
"Worked in differential topology where he proved
the generalized Poincaré conjecture in dimension
n≥5: Every closed, n-dimensional manifold homotopy-equivalent
to the n-dimensional sphere is homeomorphic to it.
Introduced the method of handle-bodies to solve this
and related problems." |
| 1970 |
Nice, France |
Alan Baker |
University of Cambridge, UK |
Trinity College, Cambridge, UK |
"Generalized the Gelfond-Schneider theorem (the
solution to Hilbert's seventh problem). From this
work he generated transcendental numbers not
previously identified." |
|
Heisuke Hironaka |
Harvard University, US |
Kyoto University, Japan |
"Generalized work of Zariski who had proved for
dimension ≤ 3 the theorem concerning the resolution
of singularities on an algebraic variety. Hironaka
proved the results in any dimension." |
|
John G. Thompson |
University of Cambridge, UK |
University of Cambridge, UK
University of Florida, US |
"Proved jointly with
W. Feit that all non-cyclic finite simple groups
have even order. The extension of this work by
Thompson determined the minimal simple finite
groups, that is, the simple finite groups whose
proper subgroups are solvable." |
|
Sergei Novikov |
Moscow State University, USSR |
Steklov Mathematical Institute, Russia
Moscow State University, Russia
University of Maryland-College Park, US |
"Made important advances in topology, the most
well-known being his proof of the topological
invariance of the Pontrjagin classes of the
differentiable manifold. His work included a study
of the cohomology and homotopy of Thom spaces."
|
| 1974 |
Vancouver, Canada |
Enrico Bombieri |
University of Pisa, Italy |
Institute for Advanced Study, US |
"Major contributions in the primes, in univalent
functions and the local Bieberbach conjecture, in
theory of functions of several complex variables,
and in theory of partial differential equations and
minimal surfaces – in particular, to the solution of
Bernstein's problem in higher dimensions." |
|
David Mumford |
Harvard University, US |
Brown University, US |
"Contributed to problems of the existence and
structure of varieties of moduli, varieties whose
points parametrize isomorphism classes of some type
of geometric object. Also made several important
contributions to the theory of algebraic surfaces."
|
| 1978 |
Helsinki, Finland |
Pierre Deligne |
Institut des Hautes Études Scientifiques, France
|
Institute for Advanced Study, US |
"Gave solution of the three Weil conjectures
concerning generalizations of the Riemann hypothesis
to finite fields. His work did much to unify
algebraic geometry and algebraic number theory."
|
|
Charles Fefferman |
Princeton University, US |
Princeton University, US |
"Contributed several innovations that revised
the study of multidimensional complex analysis by
finding correct generalizations of classical
(low-dimensional) results." |
|
Daniel Quillen |
Massachusetts Institute of Technology, US |
University of Oxford, UK |
"The prime architect of the higher algebraic
K-theory, a new tool that successfully employed
geometric and topological methods and ideas to
formulate and solve major problems in algebra,
particularly ring theory and module theory." |
|
Grigori Margulis |
Moscow State University, USSR |
Yale University, US |
"Provided innovative analysis of the structure
of Lie groups. His work belongs to combinatorics,
differential geometry, ergodic theory, dynamical
systems, and Lie groups." |
| 1982 |
Warsaw, Poland |
Alain Connes |
Institut des Hautes Études Scientifiques, France
|
Institut des Hautes Études Scientifiques, France
Collège de France, France
Ohio State University, US |
"Contributed to the theory of operator algebras,
particularly the general classification and
structure theorem of factors of type III,
classification of automorphisms of the hyperfinite
factor, classification of injective factors, and
applications of the theory of C*-algebras to
foliations and differential geometry in general."
|
|
William Thurston |
Princeton University, US |
Cornell University, US |
"Revolutionized study of topology in 2 and 3
dimensions, showing interplay between analysis,
topology, and geometry. Contributed idea that a very
large class of closed 3-manifolds carry a hyperbolic
structure." |
|
Shing-Tung Yau |
Institute for Advanced Study, US |
Harvard University, US |
"Made contributions in differential equations,
also to the Calabi conjecture in algebraic geometry,
to the positive mass conjecture of general
relativity theory, and to real and complex
Monge-Ampère equations." |
| 1986 |
Berkeley, US |
Simon Donaldson |
University of Oxford, UK |
Imperial College London, UK
Stony Brook University, US |
"Received medal primarily for his work on
topology of four-manifolds, especially for showing
that there is a differential structure on euclidian
four-space which is different from the usual
structure." |
|
Gerd Faltings |
Princeton University, US |
Max Planck Institute for Mathematics, Germany]
|
"Using methods of arithmetic algebraic geometry,
he received medal primarily for his proof of the
Mordell Conjecture." |
|
Michael Freedman |
University of California, San Diego, US |
Microsoft Station Q, US |
"Developed new methods for topological analysis
of four-manifolds. One of his results is a proof of
the four-dimensional Poincaré Conjecture." |
| 1990 |
Kyoto, Japan |
Vladimir Drinfeld |
B Verkin Institute for Low Temperature Physics and
Engineering, USSR[57]
|
University of Chicago, US |
"For his work on quantum groups and for his work
in number theory." |
|
Vaughan F. R. Jones |
University of California, Berkeley, US |
University of California, Berkeley, US,
Vanderbilt University, US |
"for his discovery of an unexpected link between
the mathematical study of knots – a field that dates
back to the 19th century – and statistical
mechanics, a form of mathematics used to study
complex systems with large numbers of components."
|
|
Shigefumi Mori |
Kyoto University, Japan |
Kyoto University, Japan |
"for the proof of Hartshorne’s conjecture and
his work on the classification of three-dimensional
algebraic varieties." |
|
Edward Witten |
Institute for Advanced Study, US |
Institute for Advanced Study, US |
"proof in 1981 of the positive energy theorem in
general relativity"[63]
|
| 1994 |
Zurich, Switzerland |
Jean Bourgain |
Institut des Hautes Études Scientifiques, France
|
Institute for Advanced Study, US |
"Bourgain's work touches on several central
topics of mathematical analysis: the geometry of
Banach spaces, convexity in high dimensions,
harmonic analysis, ergodic theory, and finally,
nonlinear partial differential equations from
mathematical physics." |
|
Pierre-Louis Lions |
University of Paris 9, France |
Collège de France, France
École polytechnique, France[6 |
"... such nonlinear partial differential
equation simply do not have smooth or even C1
solutions existing after short times. ... The only
option is therefore to search for some kind of
"weak" solution. This undertaking is in effect to
figure out how to allow for certain kinds of
"physically correct" singularities and how to forbid
others. ... Lions and Crandall at last broke open
the problem by focusing attention on viscosity
solutions, which are defined in terms of certain
inequalities holding wherever the graph of the
solution is touched on one side or the other by a
smooth test function." |
|
Jean-Christophe Yoccoz |
Paris-Sud 11 University, France |
Collège de France, France |
"proving stability properties - dynamic
stability, such as that sought for the solar system,
or structural stability, meaning persistence under
parameter changes of the global properties of the
system." |
|
Efim Zelmanov |
University of California, San Diego, US |
Steklov Mathematical Institute, Russia,
University of California, San Diego, US |
"For his solution to the restricted Burnside
problem." |
| 1998 |
Berlin, Germany |
Richard Borcherds |
University of California, Berkeley, US
University of Cambridge, UK |
University of California, Berkeley, US |
"for his work on the introduction of vertex
algebras, the proof of the Moonshine conjecture and
for his discovery of a new class of automorphic
infinite products" |
|
Timothy Gowers |
University of Cambridge, UK |
University of Cambridge, UK |
"William Timothy Gowers has provided important
contributions to functional analysis, making
extensive use of methods from combination theory.
These two fields apparently have little to do with
each other, and a significant achievement of Gowers
has been to combine these fruitfully." |
|
Maxim Kontsevich |
Institut des Hautes Études Scientifiques, France
Rutgers University, US |
Institut des Hautes Études Scientifiques, France
Rutgers University, US |
"contributions to four problems of geometry"
|
|
Curtis T. McMullen |
Harvard University, US |
Harvard University, US |
"He has made important contributions to various
branches of the theory of dynamical systems, such as
the algorithmic study of polynomial equations, the
study of the distribution of the points of a lattice
of a Lie group, hyperbolic geometry, holomorphic
dynamics and the renormalization of maps of the
interval." |
| 2002 |
Beijing, China |
Laurent Lafforgue |
Institut des Hautes Études Scientifiques, France
|
Institut des Hautes Études Scientifiques, France
|
"Laurent Lafforgue has been awarded the Fields
Medal for his proof of the Langlands correspondence
for the full linear groups
GLr (r≥1) over function fields." |
|
Vladimir Voevodsky |
Institute for Advanced Study, US |
Institute for Advanced Study, US |
" he defined and developed motivic cohomology
and the A1-homotopy theory of algebraic varieties;
he proved the Milnor conjectures on the K-theory of
fields" |
| 2006 |
Madrid, Spain |
Andrei Okounkov |
Princeton University, US |
Columbia University, US |
"for his contributions bridging probability,
representation theory and algebraic geometry" |
|
Grigori Perelman (declined) |
None |
St. Petersburg Department of Steklov Institute of
Mathematics of Russian Academy of Sciences,
Russia |
"for his contributions to geometry and his
revolutionary insights into the analytical and
geometric structure of the Ricci flow" |
|
Terence Tao |
University of California, Los Angeles, US |
University of California, Los Angeles, US |
"for his contributions to partial differential
equations, combinatorics, harmonic analysis and
additive number theory" |
|
Wendelin Werner |
Paris-Sud 11 University, France |
ETH Zurich, Switzerland |
"for his contributions to the development of
stochastic Loewner evolution, the geometry of
two-dimensional Brownian motion, and conformal field
theory" |
| 2010 |
Hyderabad, India |
Elon Lindenstrauss |
Hebrew University of Jerusalem, Israel
Princeton University, US |
Hebrew University of Jerusalem, Israel |
"For his results on measure rigidity in ergodic
theory, and their applications to number theory."
|
|
Ngô Bảo Châu |
Paris-Sud 11 University, France
Institute for Advanced Study, US |
University of Chicago, US
Vietnam Institute for Advanced Study, Vietnam |
"For his proof of the Fundamental Lemma in the
theory of automorphic forms through the introduction
of new algebro-geometric methods" |
|
Stanislav Smirnov |
University of Geneva, Switzerland |
University of Geneva, Switzerland
St. Petersburg State University, Russia |
"For the proof of conformal invariance of
percolation and the planar Ising model in
statistical physics" |
|
Cédric Villani |
École Normale Supérieure de Lyon, France
Institut Henri Poincaré, France |
Lyon University, France
Institut Henri Poincaré, France |
"For his proofs of nonlinear Landau damping and
convergence to equilibrium for the Boltzmann
equation." |
| 2014 |
Seoul, South Korea |
Artur Avila |
University of Paris VII, France
CNRS, France
Instituto Nacional de Matemática Pura e Aplicada,
Brazil |
University of Paris VII, France
CNRS, France
Instituto Nacional de Matemática Pura e Aplicada,
Brazil |
"for his profound contributions to dynamical
systems theory, which have changed the face of the
field, using the powerful idea of renormalization as
a unifying principle." |
|
Manjul Bhargava |
Princeton University, US |
Princeton University, US |
"for developing powerful new methods in the
geometry of numbers, which he applied to count rings
of small rank and to bound the average rank of
elliptic curves." |
|
Martin Hairer |
University of Warwick, UK |
Imperial College London, UK |
"for his outstanding contributions to the theory
of stochastic partial differential equations, and in
particular for the creation of a theory of
regularity structures for such equations." |
|
Maryam Mirzakhani |
Stanford University, US |
Stanford University, US |
"for her outstanding contributions to the
dynamics and geometry of Riemann surfaces and their
moduli spaces." |
| 2018 |
Rio de Janeiro, Brazil |
Caucher Birkar |
University of Cambridge, UK |
University of Cambridge, UK |
"for his proof of the boundedness of Fano
varieties and for contributions to the minimal model
program".[87]
|
|
Alessio Figalli |
Swiss Federal Institute of Technology Zurich,
Switzerland |
Swiss Federal Institute of Technology Zurich,
Switzerland |
"for his contributions to the theory of optimal
transport, and its application to partial
differential equations, metric geometry, and
probability" |
|
Peter Scholze |
University of Bonn, Germany |
University of Bonn, Germany |
"for transforming arithmetic algebraic geometry
over p-adic fields through his introduction of
perfectoid spaces, with application to Galois
representations and for the development of new
cohomology theories." |
|
Akshay Venkatesh |
Stanford University, US |
Stanford University, US
Institute for Advanced Study, US[88]
|
"for his synthesis of analytic number theory,
homogeneous dynamics, topology, and representation
theory, which has resolved long-standing problems in
areas such as the equidistribution of arithmetic
objects." |
Landmarks[edit]
In 1954,
Jean-Pierre Serre became the youngest winner of the
Fields Medal, at 27. He still retains this distinction.
In 1966,
Alexander Grothendieck boycotted the ICM, held in
Moscow, to protest Soviet military actions taking place in
Eastern Europe.[89]
Léon Motchane, founder and director of the
Institut des Hautes Études Scientifiques attended and
accepted Grothendieck's Fields Medal on his behalf.[90]
In 1970,
Sergei Novikov, because of restrictions placed on him by
the Soviet government, was unable to travel to the congress
in
Nice to receive his medal.
In 1978,
Grigory Margulis, because of restrictions placed on him
by the Soviet government, was unable to travel to the
congress in
Helsinki to receive his medal. The award was accepted on
his behalf by
Jacques Tits, who said in his address: "I cannot but
express my deep disappointment—no doubt shared by many
people here—in the absence of Margulis from this ceremony.
In view of the symbolic meaning of this city of Helsinki, I
had indeed grounds to hope that I would have a chance at
last to meet a mathematician whom I know only through his
work and for whom I have the greatest respect and
admiration."
In 1982, the congress was due to be held in
Warsaw but had to be rescheduled to the next year,
because of
martial law introduced in Poland on 13 December 1981.
The awards were announced at the ninth General Assembly of
the IMU earlier in the year and awarded at the 1983 Warsaw
congress.
In 1990,
Edward Witten became the first
physicist to win this award.
In 1998, at the ICM,
Andrew Wiles was presented by the chair of the Fields
Medal Committee,
Yuri I. Manin, with the first-ever IMU silver plaque in
recognition of his proof of
Fermat's Last Theorem.
Don Zagier referred to the plaque as a "quantized Fields
Medal". Accounts of this award frequently make reference
that at the time of the award Wiles was over the age limit
for the Fields medal. Although Wiles was slightly over the
age limit in 1994, he was thought to be a favorite to win
the medal; however, a gap (later resolved by
Taylor and Wiles) in the proof was found in 1993.
In 2006,
Grigori Perelman, who proved the
Poincaré conjecture, refused his Fields Medal[7]
and did not attend the congress.[95]
In 2014,
Maryam Mirzakhani became the first woman as well as the
first Iranian,
Artur Avila the first
South American and
Manjul Bhargava the first person of
Indian origins to win the Fields Medal.
Medal
The reverse of the Fields Medal
The medal was designed by Canadian sculptor
R. Tait McKenzie.
 | On the obverse is
Archimedes and a quote attributed to him which reads
in Latin: "Transire suum pectus mundoque potiri" ("Rise
above oneself and grasp the world"). The date is written
in Roman numerals and contains an error ("MCNXXXIII"
rather than "MCMXXXIII"). In capital Greek letters the
word ΑΡXIMHΔΟΥΣ, or "of Archimedes". |
| On the reverse is the inscription (in Latin): |
-
CONGREGATI
- EX
TOTO ORBE
-
MATHEMATICI
- OB
SCRIPTA INSIGNIA
-
TRIBUERE
Translation: "Mathematicians gathered from the entire
world have awarded [understood but not written: 'this
prize'] for outstanding writings."
In the background, there is the representation of
Archimedes'
tomb, with the carving illustrating his theorem
On the Sphere and Cylinder, behind a branch. (This is
the mathematical result of which Archimedes was reportedly
most proud: Given a sphere and a circumscribed cylinder of
the same height and diameter, the ratio between their
volumes is equal to ⅔.)
The rim bears the name of the prizewinner.
Gender disparity
In terms
of the most prestigious awards in
STEM fields, only a small proportion have been awarded
to women. The Fields Medal was only obtained for the first
time by a woman,
Maryam Mirzakhani from Iran, in 2014 out of a total of
(at the time) 56 medallists.
|
